|
Нейронные сети могут все. Но точно
также «все» могут машины Тьюринга, интерполяционные многочлены, схемы Поста,
ряды Фурье, рекурсивные функции, дизъюнктивные нормальные формы, сети Петри. В
предыдущей главе было показано, что с помощью нейронных сетей можно сколь
угодно точно аппроксимировать любую непрерывную функцию и имитировать любой
непрерывный автомат. Это и слишком много ‑ никому не нужен столь широкий
класс функций, и слишком мало, так как далеко не все важные задачи ставятся как
задачи аппроксимации.
Другое дело, что в конечном итоге
решение практически любой задачи можно описать, как построение некоторой
функции, перерабатывающей исходные данные в результат, но такое очень общее
описание не дает никакой информации о способе построения этой функции. Мало
иметь универсальные способности ‑ надо для каждого класса задач указать,
как применять эти способности. Именно здесь, при рассмотрении методов настройки
нейронных сетей для решения задач должны выявиться реальные рамки их
применимости. Конечно, такие реальные рамки изменяются со временем из-за
открытия новых методов и решений.
В данной главе описано несколько
базовых задач для нейронных сетей и основных или исторически первых методов
настройки сетей для их решения:
- Классификация (с учителем) (персептрон Розенблатта [1-3]).
- Ассоциативная память (сети Хопфилда [4-7]).
- Решение систем линейных уравнений (сети Хопфилда [8]).
- Восстановление пробелов в данных (сети Хопфилда).
- Кластер-анализ и классификация (без учителя) (сети Кохонена [9-12]).
Начнем мы, однако, не с сетей, а с
систем, состоящих из одного элемента.
1. Настройка одноэлементных систем для решения задач
Даже системы из одного адаптивного
сумматора находят очень широкое применение. Вычисление линейных функций
необходимо во многих задачах. Вот неполный перечень «специальностей»
адаптивного сумматора:
- Линейная регрессия и восстановление простейших закономерностей [13-14];
- Линейная фильтрация и адаптивная обработка сигналов [15];
- Линейное разделение классов и простейшие задачи распознавания образов [16-18].
Задача линейной регрессии состоит в поиске наилучшего линейного
приближения функции, заданной конечным набором значений: дана выборка значений
вектора аргументов x1 , ..., xm, заданы
значения функции F в этих точках: F(x i)=f i,
требуется найти линейную (неоднородную) функцию j(x)=(a,x)+a0,
ближайшую к F. Чтобы однозначно поставить задачу, необходимо
доопределить, что значит «ближайшую». Наиболее популярен метод наименьших квадратов, согласно которому
j ищется из условия
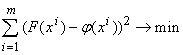 |
(1) |
Необходимо особенно подчеркнуть,
что метод наименьших квадратов не является ни единственным, ни наилучшим во
всех отношениях способом доопределения задачи регрессии. Его главное
достоинство ‑ квадратичность минимизируемого критерия и линейность
получаемых уравнений на коэффициенты j.
Явные формулы линейной регрессии легко получить, минимизируя квадратичный критерий качества регрессии.
Обозначим
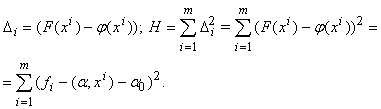
Найдем производные минимизируемой функции H по настраиваемым параметрам:
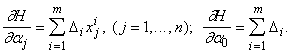
где x ij ‑ j-я координата вектора x i.
Приравнивая частные производные H нулю, получаем уравнения,
из которых легко найти все aj (j=0,...,n).
Решение удобно записать в общем виде, если для всех i =1,...,m
обозначить 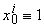 и
рассматривать n+1-мерные векторы данных x i и коэффициентов a. Тогда
и
рассматривать n+1-мерные векторы данных x i и коэффициентов a. Тогда
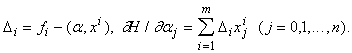
Обозначим p n+1-мерный
вектор с координатами 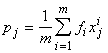 ; Q - матрицу размером (n+1)´(n+1)
с элементами
; Q - матрицу размером (n+1)´(n+1)
с элементами 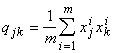 . .
В новых обозначениях решение задачи линейной регрессии имеет вид:
Приведем это решение в традиционных
обозначениях математической статистики.
Обозначим Mî среднее значение j-й
координаты векторов исходной выборки:
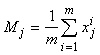 . .
Пусть M ‑ вектор с
координатами Mî.
Введем также обозначение sj для выборочного среднеквадратичного отклонения:
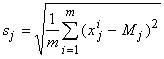
Величины sj задают естественный масштаб для измерения j-х
координат векторов x. Кроме того, нам потребуются величина sf и
коэффициенты корреляции f с j-ми координатами векторов x ‑ rfj:
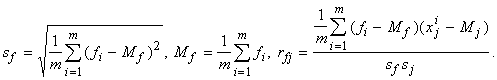
Вернемся к n-мерным векторам данных и
коэффициентов. Представим, что векторы сигналов проходят предобработку ‑
центрирование и нормировку и далее мы имеем дело с векторами y i:
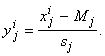
Это, в частности, означает, что все
рассматриваемые координаты вектора x имеют ненулевую дисперсию, т.е.
постоянные координаты исключаются из рассмотрения ‑ они не несут полезной
информации. Уравнения регрессии будем искать в форме: j(y)=(b,y)+b0. Получим:
где Rf
‑ вектор коэффициентов корреляции f с j-ми координатами векторов x, имеющий координаты rfj, R ‑ матрица коэффициентов
корреляции между координатами вектора
данных:
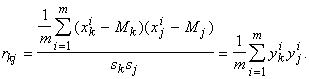
В задачах обработки данных почти
всегда возникает вопрос о последовательном уточнении результатов по мере
поступления новых данных (обработка
данных «на лету»). Существует, как минимум, два подхода к ответу на этот
вопрос для задачи линейной регрессии. Первый подход состоит в том, что
изменения в коэффициентах регрессии при поступлении новых данных
рассматриваются как малые и в их вычислении ограничиваются первыми порядками
теории возмущений. При втором подходе для каждого нового вектора данных
делается шаг изменений коэффициентов, уменьшающий ошибку регрессии D2 на вновь
поступившем векторе данных. При этом «предыдущий опыт» фиксируется только в
текущих коэффициентах регрессии.
В рамках первого подхода
рассмотрим, как будет изменяться a из формулы (2) при добавлении нового вектора данных. В
первом порядке теории возмущений найдем изменение вектора коэффициента a при
изменении вектора p и матрицы Q:
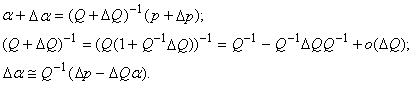
Пусть на выборке 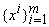 вычислены p, Q, Q‑1. При получении нового вектора данных xm+1 и
соответствующего значения F(xm+1)=fm+1 имеем 2:
вычислены p, Q, Q‑1. При получении нового вектора данных xm+1 и
соответствующего значения F(xm+1)=fm+1 имеем 2:
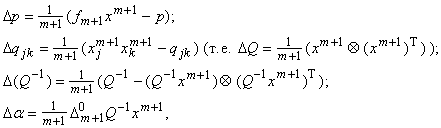 |
(4) |
где 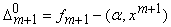 ‑ ошибка на
векторе данных xm+1 регрессионной зависимости, полученной на основании
выборки
‑ ошибка на
векторе данных xm+1 регрессионной зависимости, полученной на основании
выборки 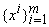 . .
Пересчитывая по приведенным
формулам p, Q, Q‑1
и a
после каждого получения данных, получаем процесс, в котором последовательно
уточняются уравнения линейной регрессии. И требуемый объем памяти, и количество
операций имеют порядок n2 ‑ из-за
необходимости накапливать и модифицировать матрицу Q‑1. Конечно,
это меньше, чем потребуется на обычное обращение матрицы Q на каждом
шаге, однако следующий простой алгоритм еще экономнее. Он вовсе не обращается к
матрицам Q, Q‑1 и основан на уменьшении на каждом шаге величины 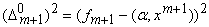 ‑ квадрата ошибки на векторе данных xm+1
регрессионной зависимости, полученной на основании выборки
‑ квадрата ошибки на векторе данных xm+1
регрессионной зависимости, полученной на основании выборки 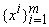 . .
Вновь обратимся к формуле (2) и
будем рассматривать n+1-мерные векторы данных и коэффициентов. Обозначим 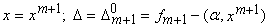 . Тогда . Тогда
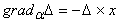 |
(5) |
Последняя элементарная формула
столь важна в теории адаптивных сумматоров, что носит «именное название» ‑
формула Уидроу. «Обучение» адаптивного сумматора методом наискорейшего спуска
состоит в изменении вектора коэффициентов a в направлении
антиградиента D2: на каждом
шаге к a
добавляется h´D´x, где h ‑ величина шага.
Если при каждом поступлении нового
вектора данных x изменять a указанным образом, то
получим последовательную процедуру построения линейной аппроксимации функции F(x). Такой
алгоритм обучения легко реализуется аппаратными средствами (изменение веса
связи aj есть произведение прошедшего по ней сигнала xj на ошибку D и на величину шага). Возникает, однако,
проблема сходимости: если h слишком мало, то сходимость будет
медленной, если же слишком велико, то произойдет потеря устойчивости и
сходимости не будет вовсе. Детальному изложению этого подхода и его приложений
посвящен учебник [15].
Задача четкого разделения двух классов по обучающей выборке ставится так: имеется два
набора векторов x1 , ..., xm и y1,...,ym . Заранее известно, что x i
относится к первому классу, а y i - ко второму. Требуется построить решающее правило, то есть определить
такую функцию f(x), что при f(x)>0
вектор x относится к первому классу,
а при f(x)<0 ‑
ко второму.
Координаты классифицируемых
векторов представляют собой значения
некоторых признаков (свойств) исследуемых объектов.
Эта задача возникает во многих
случаях: при диагностике болезней и определении неисправностей машин по
косвенным признакам, при распознавании изображений и сигналов и т.п.
Строго говоря, классифицируются не векторы свойств, а объекты, которые
обладают этими свойствами. Это замечание становится важным в тех случаях,
когда возникают затруднения с построением решающего правила - например тогда,
когда встречаются принадлежащие к разным классам объекты, имеющие одинаковые
признаки. В этих случаях возможно несколько решений:
- искать дополнительные признаки, позволяющие разделить классы;
- примириться с неизбежностью ошибок, назначить за каждый тип ошибок свой штраф
(c12 - штраф за то, что объект первого класса отнесен ко второму, c21 -
за то, что объект второго класса отнесен к первому) и строить разделяющее правило так, чтобы
минимизировать математическое ожидание штрафа;
- перейти к нечеткому разделению классов - строить так называемые "функции принадлежности"
f1(x) и f2(x) ‑ f i(x)
оценивает степень уверенности при отнесении объекта к i -му классу (i =1,2), для
одного и того же x может быть так, что и f1(x)>0,
и f2(x)>0.
Линейное
разделение классов состоит в построении
линейного решающего правила ‑ то есть такого вектора a и
числа a0 (называемого
порогом), что при (x,a)>a0 x относится к первому
классу, а при (x, a)<a0 - ко второму.
Поиск такого решающего правила
можно рассматривать как разделение классов в проекции на прямую. Вектор a
задает прямую, на которую ортогонально проектируются все точки, а число a0 ‑ точку на этой прямой, отделяющую первый класс от
второго.
Простейший и подчас очень удобный
выбор состоит в проектировании на прямую, соединяющую центры масс выборок. Центр масс вычисляется в предположении,
что массы всех точек одинаковы и равны 1. Это соответствует заданию a в
виде
| a=
(y1+ y2+...+ym)/m
‑(x1+ x2+...+ x n)/n. |
(6) |
Во многих случаях удобнее иметь
дело с векторами единичной длины. Нормируя a, получаем:
a= ((y1+ y2+...+ym)/m ‑(x1+ x2+...+ x n)/n)/||(y1+ y2+...+ym)/m ‑(x1+ x2+...+ x n)/n||.
Выбор a0
может производиться из различных соображений. Простейший вариант ‑
посередине между центрами масс выборок:
a0=(((y1+ y2+...+ym)/m,a)+((x1+ x2+...+ x n)/n,a))/2.
Более тонкие способы построения
границы раздела классов a0 учитывают
различные вероятности появления объектов разных классов, и оценки плотности
распределения точек классов на прямой. Чем меньше вероятность появления данного
класса, тем более граница раздела приближается к центру тяжести соответствующей
выборки.
Можно для каждого класса построить
приближенную плотность вероятностей распределения проекций его точек на прямую
(это намного проще, чем для многомерного распределения) и выбирать a0, минимизируя вероятность ошибки. Пусть решающее правило
имеет вид: при (x, a)>a0 x относится к первому
классу, а при (x, a)<a0 ‑ ко второму. В таком случае вероятность ошибки
будет равна
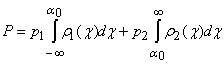
где p1, p2 ‑ априорные вероятности принадлежности объекта
соответствующему классу,
r1(c), r2(c) ‑ плотности вероятности для
распределения проекций c
точек x в каждом классе.
Приравняв нулю производную
вероятности ошибки по a0, получим:
число a0, доставляющее минимум вероятности ошибки, является корнем
уравнения:
либо (если у этого
уравнения нет решений) оптимальным является правило, относящее все объекты к
одному из классов.
Если принять гипотезу о
нормальности распределений:
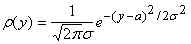 , ,
то для определения a0 получим:
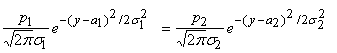 , ,
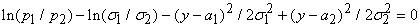
Если это уравнение имеет два корня y=a1, a2, (a1<a2) то наилучшим решающим правилом будет: при a1<(x, a)<a2 объект принадлежит одному
классу, а при a1>(x, a) или (x, a)>a2 ‑ другому (какому
именно, определяется тем, которое из произведений p ir i(c) больше). Если корней нет,
то оптимальным является отнесение к одному из классов. Случай единственного
корня представляет интерес только тогда, когда s1=s2. При этом
уравнение превращается в линейное и мы приходим к исходному варианту ‑
единственной разделяющей точке a0.
Таким образом, разделяющее правило
с единственной разделяющей точкой a0 не является
наилучшим для нормальных распределений и надо искать две разделяющие точки.
Если сразу ставить задачу об
оптимальном разделении многомерных нормальных распределений, то получим, что
наилучшей разделяющей поверхностью является квадрика (на прямой типичная
«квадрика» ‑ две точки). Предполагая, что ковариационные матрицы классов
совпадают (в одномерном случае это предположение о том, что s1=s2), получаем
линейную разделяющую поверхность. Она ортогональна прямой, соединяющей центры
выборок не в обычном скалярном произведении, а в специальном: 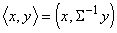 , где S ‑ общая ковариационная матрица классов. За
деталями отсылаем к прекрасно написанной книге [17], см. также [11,12,16]. , где S ‑ общая ковариационная матрица классов. За
деталями отсылаем к прекрасно написанной книге [17], см. также [11,12,16].
Важная возможность
усовершенствовать разделяющее правило состоит с использовании оценки не просто
вероятности ошибки, а среднего риска: каждой ошибке приписывается «цена» c i и минимизируется сумма c1p1r1(c)+c2p2r2(c). Ответ получается практически тем же
(всюду p i
заменяются на c ip i),
но такая добавка важна для многих приложений.
Требование
безошибочности разделяющего правила на обучающей выборке принципиально
отличается от обсуждавшихся критериев оптимальности. На основе этого требования строится персептрон Розенблатта ‑ «дедушка» современных нейронных
сетей [1].
Возьмем за основу при построении
гиперплоскости, разделяющей классы, отсутствие ошибок на обучающей выборке.
Чтобы удовлетворить этому условию, придется решать систему линейных неравенств:
(x i, a)>a0 (i =1,...,n)
(yj , a)<a0 (j=1,...,m).
Здесь x i (i =1,..,n) - векторы из обучающей выборки,
относящиеся к первому классу, а yj (j=1,..,n) - ко второму.
Удобно переформулировать задачу.
Увеличим размерности всех векторов на единицу, добавив еще одну координату ‑a0 к a, x0 =1 - ко всем x и y0 =1 ‑ ко
всем y . Сохраним для новых векторов
прежние обозначения - это не приведет к путанице.
Наконец, положим z i =x i (i =1,...,n), zj = ‑yj
(j=1,...,m).
Тогда получим систему n+m
неравенств
(z i,a)>0
(i =1,...,n+m),
которую будем решать
относительно a.
Если множество решений непусто, то любой его элемент a порождает решающее
правило, безошибочное на обучающей выборке.
Итерационный алгоритм решения этой
системы чрезвычайно прост. Он основан на том, что для любого вектора x его
скалярный квадрат (x,x) больше нуля. Пусть a ‑
некоторый вектор, претендующий на роль решения неравенств (z i,a)>0
(i =1,...,n+m), однако часть из них
не выполняется. Прибавим те z i, для
которых неравенства имеют неверный знак, к вектору a и вновь проверим все
неравенства (z i,a)>0 и т.д. Если они
совместны, то процесс сходится за конечное число шагов. Более того, добавление z i к a можно производить сразу после того, как ошибка ((z i,a)<0)
обнаружена, не дожидаясь проверки всех неравенств ‑ и этот вариант
алгоритма тоже сходится [2].
2. Сети Хопфилда
Перейдем от одноэлементных систем к
нейронным сетям. Пусть aij ‑
вес связи, ведущей от j-го нейрона к i -му (полезно обратить внимание на порядок индексов).
Для полносвязных сетей определены значения aij при всех i ,j, для других архитектур связи,
ведущие от j-го нейрона к i -му для некоторых i ,j
не определены. В этом случае положим aij=0.
В данном разделе речь пойдет в
основном о полносвязных сетях. Пусть на выходах всех нейронов получены сигналы xj (j-номер нейрона). Обозначим x вектор этих выходных
сигналов. Прохождение вектора сигналов x через сеть связей
сводится к умножению матрицы (aij) на вектор сигналов x. В
результате получаем вектор входных сигналов нелинейных элементов нейронов: 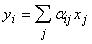 . .
Это соответствие «прохождение сети º
умножение матрицы связей на вектор сигналов» является основой для перевода
обычных численных методов на нейросетевой язык и обратно. Практически всюду,
где основной операцией является умножение матрицы на вектор, применимы
нейронные сети. С другой стороны, любое устройство, позволяющее быстро осуществлять
такое умножение, может использоваться для реализации нейронных сетей.
В частности, вычисление градиента квадратичной формы 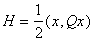 может осуществляться
полносвязной сетью с симметричной матрицей
связей:
может осуществляться
полносвязной сетью с симметричной матрицей
связей: 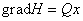 (
(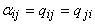 ). Именно это наблюдение лежит в основе данного раздела.
). Именно это наблюдение лежит в основе данного раздела.
Что можно сделать, если мы умеем
вычислять градиент квадратичной формы?
В первую очередь, можно методом наискорейшего спуска искать точку минимума многочлена второго
порядка. Пусть задан такой многочлен: 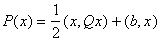 . Его градиент равен . Его градиент равен 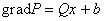 . Этот вектор может быть получен при прохождении вектора x через
сеть с весами связей . Этот вектор может быть получен при прохождении вектора x через
сеть с весами связей 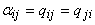 при условии, что на
входной сумматор каждого нейрона по дополнительной связи веса b подается
стандартный единичный сигнал.
при условии, что на
входной сумматор каждого нейрона по дополнительной связи веса b подается
стандартный единичный сигнал.
Зададим теперь функционирование
сети формулой
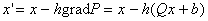 |
(8) |
Нелинейных элементов вовсе не
нужно! Каждый (j-й) нейрон имеет входные веса 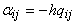 для связей с другими
нейронами (i ¹j),
вес
для связей с другими
нейронами (i ¹j),
вес 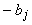 для постоянного
единичного входного сигнала и вес
для постоянного
единичного входного сигнала и вес 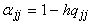 для связи нейрона с
самим собой (передачи на него его же сигнала с предыдущего шага). Выбор шага h>0 может вызвать
затруднение (он зависит от коэффициентов минимизируемого многочлена). Есть,
однако, простое решение: в каждый момент дискретного времени T выбирается свое значение
для связи нейрона с
самим собой (передачи на него его же сигнала с предыдущего шага). Выбор шага h>0 может вызвать
затруднение (он зависит от коэффициентов минимизируемого многочлена). Есть,
однако, простое решение: в каждый момент дискретного времени T выбирается свое значение 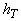 . Достаточно, чтобы шаг стремился со временем к нулю, а сумма
шагов ‑ к бесконечности (например, . Достаточно, чтобы шаг стремился со временем к нулю, а сумма
шагов ‑ к бесконечности (например, 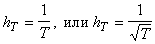 ).
).
Итак, простая симметричная
полносвязная сеть без нелинейных элементов может методом наискорейшего спуска
искать точку минимума квадратичного многочлена.
Решение системы линейных уравнений 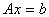 сводится к
минимизации многочлена
сводится к
минимизации многочлена
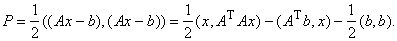
Поэтому решение
системы может производиться нейронной сетью. Простейшая сеть, вычисляющая
градиент этого многочлена, не полносвязна, а состоит из двух слоев: первый с
матрицей связей 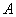 , второй ‑ с транспонированной матрицей , второй ‑ с транспонированной матрицей 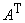 . Постоянный единичный сигнал подается на связи с весами . Постоянный единичный сигнал подается на связи с весами 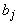 на первом слое.
Минимизация этого многочлена, а значит и решение системы линейных уравнений,
может проводиться так же, как и в общем случае, в соответствии с формулой
на первом слое.
Минимизация этого многочлена, а значит и решение системы линейных уравнений,
может проводиться так же, как и в общем случае, в соответствии с формулой 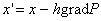 . Усовершенствованные варианты алгоритма решения можно найти
в работах Сударикова [8]. . Усовершенствованные варианты алгоритма решения можно найти
в работах Сударикова [8].
Небольшая модификация позволяет
вместо безусловного минимума многочлена второго порядка P искать точку условного
минимума с условиями 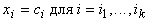 , то есть точку минимума P в ограничении на аффинное многообразие,
параллельное некоторым координатным плоскостям. Для этого вместо формулы , то есть точку минимума P в ограничении на аффинное многообразие,
параллельное некоторым координатным плоскостям. Для этого вместо формулы
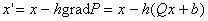
следует использовать:
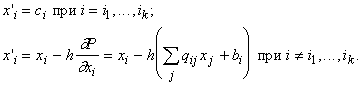 |
(9) |
Устройство, способное находить точку условного минимума многочлена
второго порядка при условиях вида 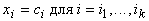 позволяет решать
важную задачу ‑ заполнять пробелы
в данных (и, в частности, строить линейную регрессию).
позволяет решать
важную задачу ‑ заполнять пробелы
в данных (и, в частности, строить линейную регрессию).
Предположим, что получаемые в ходе
испытаний векторы данных подчиняются многомерному нормальному распределению:
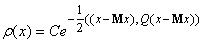 , ,
где Mx ‑ вектор математических ожиданий координат, 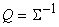 , , 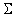 ‑ ковариационная
матрица, n ‑ размерность пространства данных,
‑ ковариационная
матрица, n ‑ размерность пространства данных,
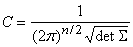 . .
Напомним определение матрицы 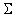 :
:
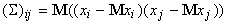 , ,
где M ‑ символ
математического ожидания, нижний индекс соответствует номеру координаты.
В частности, простейшая оценка
ковариационной матрицы по выборке дает:
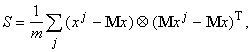
где m ‑ число
элементов в выборке, верхний индекс j ‑ номер вектора
данных в выборке, верхний индекс Т означает транспонирование, а Ä
‑ произведение вектора-столбца на вектор-строку (тензорное произведение).
Пусть у вектора данных x известно несколько координат: 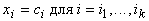 . Наиболее вероятные значения неизвестных координат должны
доставлять условный максимум показателю нормального распределения ‑
многочлену второго порядка . Наиболее вероятные значения неизвестных координат должны
доставлять условный максимум показателю нормального распределения ‑
многочлену второго порядка 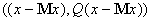 (при условии
(при условии 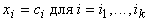 ). Эти же значения будут условными математическими ожиданиями
неизвестных координат при заданных условиях.
). Эти же значения будут условными математическими ожиданиями
неизвестных координат при заданных условиях.
Таким образом, чтобы построить
сеть, заполняющую пробелы в данных, достаточно сконструировать сеть для поиска
точек условного минимума многочлена 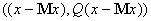 при условиях
следующего вида:
при условиях
следующего вида: 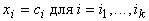 . Матрица связей Q выбирается из условия . Матрица связей Q выбирается из условия 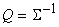 , где S ‑ ковариационная матрица (ее оценка по выборке). , где S ‑ ковариационная матрица (ее оценка по выборке).
На первый взгляд, пошаговое
накопление 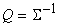 по мере поступления
данных требует слишком много операций ‑ получив новый вектор данных
требуется пересчитать оценку S, а потом вычислить
по мере поступления
данных требует слишком много операций ‑ получив новый вектор данных
требуется пересчитать оценку S, а потом вычислить 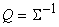 . Можно поступать и по-другому, воспользовавшись формулой
приближенного обрашения матриц первого порядка точности: . Можно поступать и по-другому, воспользовавшись формулой
приближенного обрашения матриц первого порядка точности:
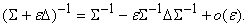
Если же добавка D
имеет вид 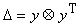 , то , то
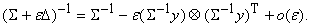 |
(10) |
Заметим, что решение задачи (точка
условного минимума многочлена) не меняется при умножении Q на число. Поэтому полагаем:
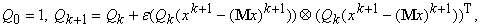
где 1 ‑
единичная матрица, e>0 ‑ достаточно
малое число, 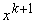 ‑ k+1-й
вектор данных,
‑ k+1-й
вектор данных, 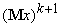 ‑ среднее
значение вектора данных, уточненное с учетом
‑ среднее
значение вектора данных, уточненное с учетом 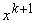 :
:
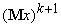 =
= 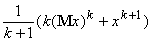
В формуле для пошагового накопления
матрицы Q ее изменение DQ при появлении новых данных
получается с помощью вектора y=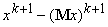 , пропущенного через сеть: , пропущенного через сеть: 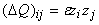 , где z=Qy. Параметр e
выбирается достаточно малым для того, чтобы обеспечить положительную
определенность получаемых матриц (и, по возможности, их близость к истинным
значениям Q). , где z=Qy. Параметр e
выбирается достаточно малым для того, чтобы обеспечить положительную
определенность получаемых матриц (и, по возможности, их близость к истинным
значениям Q).
Описанный процесс формирования сети
можно назвать обучением. Вообще говоря, можно проводить формальное различение
между формированием сети по явным формулам
и по алгоритмам, не использующим явных формул для весов связей (неявным). Тогда термин «обучение»
предполагает неявные алгоритмы, а для явных остается название «формирование».
Здесь мы такого различия проводить не будем.
Если при обучении сети поступают некомплектные данные 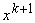 с отсутствием значений
некоторых координат, то сначала эти значения восстанавливаются с помощью
имеющейся сети, а потом используются в ее дальнейшем обучении.
с отсутствием значений
некоторых координат, то сначала эти значения восстанавливаются с помощью
имеющейся сети, а потом используются в ее дальнейшем обучении.
Во всех задачах оптимизации
существенную роль играет вопрос о правилах
остановки: когда следует прекратить циклическое функционирование сети,
остановиться и считать полученный результат ответом? Простейший выбор ‑
остановка по малости изменений: если изменения сигналов сети за цикл меньше
некоторого фиксированного малого d (при использовании переменного шага d
может быть его функцией),
то оптимизация заканчивается.
До сих пор речь шла о минимизации
положительно определенных квадратичных форм и многочленов второго порядка.
Однако самое знаменитое приложение полносвязных сетей связано с увеличением
значений положительно определенных квадратичных форм. Речь идет о системах ассоциативной памяти [4-7,9,10,12].
Предположим, что задано несколько
эталонных векторов данных 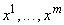 и при обработке
поступившего на вход системы вектора x требуется получить на выходе ближайший
к нему эталонный вектор. Мерой сходства в простейшем случае будем считать
косинус угла между векторами ‑ для векторов фиксированной длины это
просто скалярное произведение. Можно ожидать, что изменение вектора x по
закону
и при обработке
поступившего на вход системы вектора x требуется получить на выходе ближайший
к нему эталонный вектор. Мерой сходства в простейшем случае будем считать
косинус угла между векторами ‑ для векторов фиксированной длины это
просто скалярное произведение. Можно ожидать, что изменение вектора x по
закону
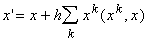 , , |
(11) |
где h ‑ малый
шаг, приведет к увеличению проекции x на те эталоны, скалярное произведение
на которые 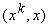 больше.
больше.
Ограничимся рассмотрением эталонов,
и ожидаемых результатов обработки с координатами  . Развивая изложенную идею, приходим к дифференциальному
уравнению . Развивая изложенную идею, приходим к дифференциальному
уравнению
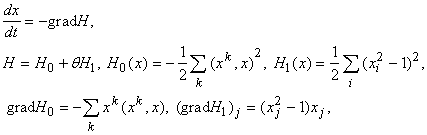 |
(12) |
где верхними
индексами обозначаются номера векторов-эталонов, нижними ‑ координаты
векторов.
Функция H называется «энергией» сети, она минимизируется в
ходе функционирования. Слагаемое 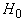 вводится для того,
чтобы со временем возрастала проекция вектора x на те эталоны, которые к
нему ближе, слагаемое
вводится для того,
чтобы со временем возрастала проекция вектора x на те эталоны, которые к
нему ближе, слагаемое 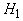 обеспечивает
стремление координат вектора x к
обеспечивает
стремление координат вектора x к 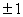 . Параметр q определяет соотношение между интенсивностями этих двух
процессов. Целесообразно постепенно менять q со временем, начиная с
малых q<1, и приходя в конце
концов к q>1. . Параметр q определяет соотношение между интенсивностями этих двух
процессов. Целесообразно постепенно менять q со временем, начиная с
малых q<1, и приходя в конце
концов к q>1.
Подробнее системы ассоциативной
памяти рассмотрены в отдельной главе. Здесь же мы ограничимся обсуждением
получающихся весов связей. Матрица связей построенной сети определяется
функцией 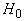 , так как , так как 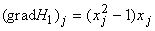 вычисляется
непосредственно при j-м нейроне без участия сети. Вес связи между i -м и j-м
нейронами не зависит от направления связи и равен
вычисляется
непосредственно при j-м нейроне без участия сети. Вес связи между i -м и j-м
нейронами не зависит от направления связи и равен
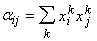 |
(13) |
Эта простая формула имеет
чрезвычайно важное значение для развития теории нейронных сетей. Вклад k-го
эталона в связь между i -м и j-м нейронами (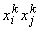 ) равен +1, если i -я и
j-я
координаты этого эталона имеют одинаковый знак, и равен ‑1, если они
имеют разный знак.
) равен +1, если i -я и
j-я
координаты этого эталона имеют одинаковый знак, и равен ‑1, если они
имеют разный знак.
В результате возбуждение i -го
нейрона передается j-му (и симметрично, от j-го к i -му), если у большинства эталонов знак i -й и j-й координат совпадают. В противном случае эти
нейроны тормозят друг друга: возбуждение i -го ведет к торможению j-го, торможение i -го ‑ к возбуждению j-го (воздействие j-го на i -й
симметрично). Это правило образования ассоциативных связей (правило Хебба)
сыграло огромную роль в теории нейронных сетей.
3. Сети Кохонена для кластер-анализа и классификации без учителя
Построение
отношений на множестве объектов - одна из самых загадочных и открытых для
творчества областей применения искусственного интеллекта. Первым и наиболее
распространенным примером этой задачи является классификация без учителя. Задан
набор объектов, каждому объекту сопоставлен вектор значений признаков (строка
таблицы). Требуется разбить эти объекты на классы эквивалентности.
Естественно, прежде, чем приступать
к решению этой задачи, нужно ответить на один вопрос: зачем производится это
разбиение и что мы будем делать с его результатом? Ответ на него позволит
приступить к формальной постановке задачи, которая всегда требует компромисса
между сложностью решения и точностью формализации: буквальное следование
содержательному смыслу задачи нередко порождает сложную вычислительную
проблему, а следование за простыми и элегантными алгоритмами может привести к
противоречию со здравым смыслом.
Итак, зачем нужно строить отношения
эквивалентности между объектами? В первую очередь - для фиксации знаний. Люди
накапливают знания о классах объектов - это практика многих тысячелетий,
зафиксированная в языке: знание относится к имени класса (пример стандартной
древней формы: "люди смертны", "люди" - имя класса). В
результате классификации как бы появляются новые имена и правила их присвоения.
Для каждого нового объекта мы
должны сделать два дела:
- найти класс, к которому он принадлежит;
- использовать новую информацию, полученную об этом объекте, для исправления (коррекции)
правил классификации.
Какую форму могут иметь правила
отнесения к классу? Веками освящена традиция представлять класс его
"типичным", "средним", "идеальным" и т.п.
элементом. Этот типичный объект является идеальной конструкцией, олицетворяющей
класс.
Отнесение объекта к классу
проводится путем его сравнения с типичными элементами разных классов и выбора
ближайшего. Правила, использующие типичные объекты и меры близости для их
сравнения с другими, очень популярны и сейчас.
Простейшая мера близости объектов -
квадрат евклидового расстояния между векторами значений их признаков (чем меньше расстояние ‑
расстояние - тем ближе объекты). Соответствующее определение признаков
типичного объекта - среднее арифметическое значение признаков по выборке,
представляющей класс.
Мы не оговариваем специально
существование априорных
ограничений, налагаемых на новые объекты -
естественно, что "вселенная" задачи много 'уже и гораздо определеннее Вселенной.
Другая мера близости, естественно
возникающая при обработке сигналов, изображений и т.п. - квадрат коэффициента
корреляции (чем он больше, тем ближе объекты). Возможны и иные варианты - все
зависит от задачи.
Если число классов m заранее определено, то задачу
классификации без учителя можно поставить следующим образом.
Пусть {xp
} - векторы значений признаков для рассматриваемых объектов и в пространстве таких векторов определена мера их близости r{x,y}. Для определенности примем, что чем
ближе объекты, тем меньше r. С каждым классом будем связывать его типичный объект. Далее называем его
ядром класса. Требуется определить
набор из m ядер y1 , y2 , ... ym
и разбиение {xp} на классы:
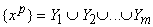
минимизирующее следующий критерий
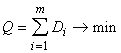 . . |
(14) |
где для каждого (i -го)
класса 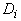 ‑ сумма
расстояний от принадлежащих ему точек выборки до ядра класса:
‑ сумма
расстояний от принадлежащих ему точек выборки до ядра класса:
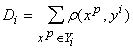 . . |
(15) |
Минимум Q берется по всем возможным положениям ядер 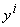 и всем разбиениям {xp}на m
классов Y i.
и всем разбиениям {xp}на m
классов Y i.
Если число классов заранее не
определено, то полезен критерий слияния классов: классы Y i
и Yj сливаются, если их ядра ближе, чем среднее расстояние от
элемента класса до ядра в одном из
них. (Возможны
варианты: использование среднего расстояния по обоим классам, использование
порогового коэффициента, показывающего, во сколько раз должно расстояние между
ядрами превосходить среднее расстояние от элемента до ядра и др.)
Использовать критерий слияния
классов можно так: сначала принимаем гипотезу о достаточном числе классов,
строим их, минимизируя Q, затем некоторые Y i
объединяем, повторяем минимизацию Q с новым числом классов и т.д.
Существует много эвристических алгоритмов классификации без учителя,
основанных на использовании мер близости между объектами. Каждый из них имеет
свою область применения, а наиболее распространенным недостатком является
отсутствие четкой формализации задачи: совершается переход от идеи кластеризации
прямо к алгоритму, в результате неизвестно, что ищется (но что-то в любом
случае находится, иногда - неплохо). Сетевые алгоритмы классификации без
учителя строятся на основе итерационного метода динамических ядер. Опишем его
сначала в наиболее общей абстрактной форме. Пусть задана выборка
предобработанных векторов данных {xp}. Пространство
векторов данных обозначим E. Каждому
классу будет соответствовать некоторое ядро a.
Пространство ядер будем обозначать A.
Для каждых xÎE и aÎA определяется мера близости d(x,a). Для каждого набора из k ядер a1,...,ak и любого разбиения {xp} на k классов {xp}=P1ÈP2È...ÈPk определим
критерий качества:
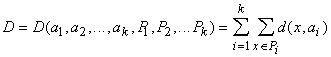 |
(16) |
Требуется найти набор a1,...,ak
и разбиение {xp}=P1ÈP2È...ÈPk, минимизирующие
D.
Шаг алгоритма разбивается на два
этапа:
1-й этап - для фиксированного
набора ядер a1,...,ak ищем минимизирующее
критерий качества D разбиение {xp}=P1ÈP2È...ÈPk; оно
дается решающим правилом: xÎP i, если d(x,a i )<d(x ,aj ) при i ¹j, в том случае, когда для x минимум d(x,a)
достигается при нескольких значениях i , выбор между ними может быть сделан
произвольно;
2-й этап - для каждого P i (i =1,...,k), полученного на первом этапе, ищется a iÎA,
минимизирующее критерий качества (т.е.
слагаемое в D для данного i - 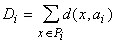
Начальные значения a1,...,ak, {xp}=P1ÈP2È...ÈPk выбираются произвольно,
либо по какому-нибудь эвристическому правилу.
На каждом шаге и этапе алгоритма
уменьшается критерий качества D, отсюда следует сходимость алгоритма -
после конечного числа шагов разбиение
{xp}=P1ÈP2È...ÈPk уже не меняется.
Если ядру a i
сопоставляется элемент сети, вычисляющий по
входному сигналу x функцию d(x,a i), то решающее правило для классификации дается
интерпретатором "победитель забирает все": элемент x принадлежит классу P i,
если выходной сигнал i -го элемента d(x,a i)
меньше всех остальных
Единственная вычислительная
сложность в алгоритме может состоять
в поиске ядра по классу на втором этапе алгоритма, т.е. в поиске aÎA, минимизирующего 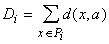
В связи с этим, в большинстве
конкретных реализаций метода мера
близости d выбирается такой, чтобы
легко можно было найти a, минимизирующее D для данного P .
В простейшем случае пространство
ядер A совпадает с пространством
векторов x, а мера близости d(x,a)
- положительно определенная квадратичная форма от x‑a, например,
квадрат евклидового расстояния или другая положительно определенная
квадратичная форма. Тогда ядро a i,
минимизирующее D i, есть центр тяжести класса P i :
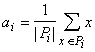 , , |
(17) |
где |P i| ‑ число элементов в P i.
В этом случае также упрощается и
решающее правило, разделяющее классы. Обозначим d(x,a)=(x-a,x-a), где (.,.) ‑ билинейная форма
(если d - квадрат евклидового
расстояния между x и a, то (.,.) - обычное скалярное
произведение). В силу билинейности
d(x,a)=(x‑a,x‑a)=(x,x)‑2(x,a)+(a,a).
Чтобы сравнить d(x,a i)
для разных i и найти среди них минимальное, достаточно вычислить
линейную неоднородную функцию от x:
d1(x,a i) = (a i,a i)‑2(x,a i).
Минимальное значение d(x,a i) достигается при том же i , что и минимум d1(x,a i), поэтому
решающее правило реализуется с помощью
k сумматоров, вычисляющих d(x,a) и интерпретатора, выбирающего сумматор с минимальным
выходным сигналом. Номер этого
сумматора и есть номер класса, к которому относится x.
Пусть теперь мера близости - коэффициент корреляции между вектором данных и ядром класса:
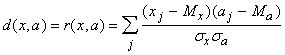
где 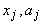 ‑ координаты векторов,
‑ координаты векторов, 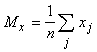 (и аналогично
(и аналогично 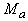 ), n ‑ размерность пространства
данных,
), n ‑ размерность пространства
данных, 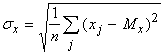 (и аналогично
(и аналогично 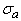 ).
).
Предполагается, что данные
предварительно обрабатываются (нормируются и центрируются) по правилу:
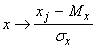 . .
Точно также нормированы и
центрированы векторы ядер a. Поэтому все обрабатываемые векторы и
ядра принадлежат сечению единичной евклидовой сферы (||x||=1)
гиперплоскостью (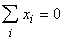 ). В таком
случае
). В таком
случае 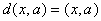 . .
Задача поиска ядра для данного
класса P имеет
своим решением
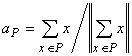 . . |
(18) |
В описанных простейших случаях,
когда ядро класса точно определяется как среднее арифметическое (или
нормированное среднее арифметическое) элементов класса, а решающее правило
основано на сравнении выходных сигналов линейных адаптивных сумматоров, нейронную
сеть, реализующую метод динамических ядер, называют сетью Кохонена. В определении
ядер a для сетей Кохонена входят
суммы 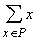 . Это позволяет накапливать новые динамические ядра,
обрабатывая по одному примеру и пересчитывая a i после появления в P i нового примера. Сходимость при такой модификации,
однако, ухудшается. . Это позволяет накапливать новые динамические ядра,
обрабатывая по одному примеру и пересчитывая a i после появления в P i нового примера. Сходимость при такой модификации,
однако, ухудшается.
Закончим раздел рассмотрением
различных способов использования полученных классификаторов.
1. Базовый способ: для вектора данных x i и каждого ядра a i вычисляется y i=d(x,a i) (условимся считать, что правильному ядру отвечает
максимум d, изменяя, если надо, знак
d); по правилу «победитель забирает все» строка ответов y i преобразуется в строку, где только один элемент,
соответствующий максимальному y i, равен 1,
остальные ‑ нули. Эта строка и является результатом функционирования
сети. По ней может быть определен номер класса (номер места, на котором стоит
1) и другие показатели.
2. Метод аккредитации: за слоем элементов базового метода, выдающих
сигналы 0 или 1 по правилу "победитель забирает все" (далее называем
его слоем базового интерпретатора), надстраивается еще один слой выходных
сумматоров. С каждым (i -м) классом
ассоциируется q-мерный выходной вектор z i с
координатами z ij . Он может формироваться по-разному: от двоичного
представления номера класса до вектора ядра класса. Вес связи, ведущей от i -го элемента слоя базового
интерпретатора к j-му выходному
сумматору определяется в точности как z ij . Если на
этом i -м элементе базового
интерпретатора получен сигнал 1, а на остальных - 0, то на выходных сумматорах
будут получены числа z ij.
3. Нечеткая классификация. Пусть для вектор данных x обработан слоем элементов, вычисляющих
y i=d(x,a i). Идея дальнейшей обработки
состоит в том, чтобы выбрать из этого набора {y i} несколько самых больших чисел и
после нормировки объявить их значениями функций принадлежности к соответствующим классам.
Предполагается, что к остальным классам
объект наверняка не принадлежит. Для выбора
семейства G наибольших y i определим
следующие числа:
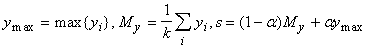
где число a характеризует отклонение
"уровня среза" s от среднего
значения 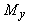 aÎ[-1,1],
по умолчанию обычно принимается a=0.
aÎ[-1,1],
по умолчанию обычно принимается a=0.
Множество J={i |y iÎG}
трактуется как совокупность номеров тех классов, к которым может принадлежать
объект, а нормированные на
единичную сумму неотрицательные величины
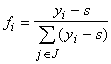 (при i ÎJ и f = 0 в противном
случае)
(при i ÎJ и f = 0 в противном
случае)
интерпретируются как значения функций принадлежности этим классам.
4. Метод интерполяции надстраивается над нечеткой классификацией аналогично тому, как
метод аккредитации связан с
базовым способом. С каждым классом связывается q-мерный выходной
вектор z i. Строится слой из q выходных сумматоров, каждый из которых должен выдавать свою компоненту выходного вектора. Весовые
коэффициенты связей, ведущих от
того элемента нечеткого классификатора,
который вычисляет f i, к j-му выходному сумматору определяются
как z ij. В итоге вектор выходных сигналов сети есть
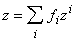
В отдельных случаях по смыслу
задачи требуется нормировка f i на
единичную сумму квадратов или
модулей.
Выбор одного из описанных четырех
вариантов использования сети (или какого-нибудь другого) определяется нуждами
пользователя. Предлагаемые четыре способа покрывают большую часть потребностей.
За пределами этой главы остался
наиболее универсальный способ обучения нейронных сетей методами гладкой
оптимизации ‑ минимизации функции оценки. Ему посвящена следующая глава.
Работа над главой была поддержана
Красноярским краевым фондом науки, грант 6F0124.
Литература
- Розенблатт Ф. Принципы нейродинамики. Перцептрон и теория механизмов мозга. М.: Мир, 1965. 480 с.
- Минский М., Пайперт С. Персептроны. - М.: Мир, 1971.
- Ивахненко А.Г. Персептроны. - Киев: Наукова думка, 1974.
- Hopfield J.J. Neural Networks and Physical systems with emergent collective
computational abilities//Proc. Nat. Sci. USA. 1982. V.79. P. 2554-2558.
- Уоссермен Ф. Нейрокомпьютерная техника.- М.: Мир, 1992.
- Итоги науки и техники. Сер. "Физ. и Матем. модели
нейронных сетей" / Под ред. А.А.Веденова. - М.: Изд-во ВИНИТИ, 1990-92 - Т. 1-5.
- Фролов А.А., Муравьев И.П. Нейронные модели ассоциативной памяти.- М.: Наука, 1987.- 160 с.
- Cудариков В.А. Исследование адаптивных нейросетевых алгоритмов решения задач линейной алгебры
// Нейрокомпьютер, 1992. № 3,4. С. 13-20.
- Кохонен Т. Ассоциативная память. - М.: Мир, 1980.
- Кохонен Т. Ассоциативные запоминающие устройства. - М.: Мир, 1982.
- Фор А. Восприятие и распознавание образов.- М.: Машиностроение, 1989.- 272 с.
- Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере.
Новосибирск: Наука (Сиб. отделение), 1996. 276 с.
- Кендалл М., Стьюарт А. Статистические выводы и связи.- М.: Наука, 1973.- 900 с.
- Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия.- М.: Финансы и статистика, 1982.- 239 с.
- Уидроу Б., Стирнз С. Адаптивная обработка сигналов. М.: Мир, 1989. 440 с.
- Айвазян С.А., Бежаева З.И., Староверов О.В. Классификация
многомерных наблюдений.- М.: Статистика, 1974.- 240 с.
- Дуда Р., Харт П. Распознавание образов и анализ сцен.- М.: Мир, 1976.- 512 с.
- Ивахненко А.Г. Самообучающиеся системы распознавания и
автоматического регулирования.- Киев: Техника, 1969.- 392 с.
- Искусственный интеллект: В 3-х кн. Кн. 2. Модели и методы:
Справочник / под ред. Д.А. Поспелова.- М.: Радио и связь, 1990.- 304 с.
- Zurada J. M. Introduction to artificial neural systems. PWS
Publishing Company, 1992. 785 P.
- Горбань А.Н. Обучение нейронных
сетей. М.: изд. СССР-США СП "ПараГраф", 1990. 160 с.
1 660036, Красноярск-36, ВЦК СО РАН. E-mail:
2 Напомним, что для векторов x, y матрица xÄyT
имеет своими элементами xjyk.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки