|
Рассматриваются нейронные сети слоистой структуры, состоящие из слоев
стандартных нейронов. Изучаются ошибки, возникающие при технической реализации
сетей, а также при шумах и повреждениях.
Определены максимально допустимые погрешности, возможные для сигналов и
параметров каждого элемента сети, исходя из условия, что вектор выходных
сигналов сети должен вычисляться с заданной точностью. Используются два типа
оценок погрешности: гарантированные
интервальные оценки и среднеквадратические оценки погрешностей.
Показано, что оценки допустимых погрешностей можно получить в ходе
специального процесса “обратного распространения точности”. Он состоит в
функционировании сети с той же системой связей, но от выходов к входам и с
заменой элементов на двойственные. Эта двойственность принципиально отличается
от той, которая используется в классическом методе вычисления градиентов оценки
с помощью обратного распространения ошибок (back propagation of errors).
С помощью полученных результатов объясняется наблюдаемая высокая
устойчивость нейронных сетей к шумам и разрушениям.
1. Введение
В настоящее
время существуют различные технические реализации нейронных сетей, в том числе
нейроимитаторы, то есть компьютерные модели нейронных сетей. Нейроимитаторы
являются гибкими средствами для изучения сетей и работы с ними. С
нейроимитаторами можно выполнять различные операции – обучать, определять
наиболее и наименее значимые связи, контрастировать, то есть удалять наименее
значимые связи и т. д.
Существует
подход, получающий все большее распространение, при котором сначала
конструируется и обучается нейроимитатор, а затем создается техническая
реализация полученной нейросети с уже вычисленными весами синапсов.
Нейроимитатор,
работающий на универсальных цифровых ЭВМ, позволяет вычислять веса синапсов с
большой точностью, которую трудно получить при других технических реализациях
сети (в первую очередь – аналоговых) в силу ограниченной точности технических
устройств. Поэтому возникает задача приведения весов синапсов к некоторому
набору конкретных значений. Ее частный случай ‑ задача бинаризации, то
есть задача приведения весов синапсов к значениям 0 или 1 (связь либо есть,
либо нет ‑ без всяких весов синапсов).
При аналоговых
реализациях, различных упрощениях архитектуры (в том числе ‑ бинаризации)
технически сложно получить результат работы сети той же точности, что и
результат работы нейроимитатора [3-5]. Поэтому следует ограничится некоторой
точностью, с которой может работать сеть, то есть выбрать интервал, в котором
могут изменяться значения вектора выходных сигналов сети.
Оценка
погрешностей сигналов сети очень полезна при решении задачи упрощения нейронной
сети. Зная допустимую погрешность выходного сигнала какого-либо элемента сети,
мы можем заменять его более простыми, но менее точными элементами так, чтобы в
итоге ошибка не превышала заданную.
Хорошо известно,
что нейронные сети могут проявлять исключительную устойчивость к помехам и
разрушениям. Иногда эти эффекты называют голографическими свойствами нейронных
сетей, подразумевая, что полезные навыки распределены по сети примерно так же,
как изображение ‑ по голографической пластинке, и могут сохраняться при
значительных разрушениях.
Как будет
показано ниже, при прямом прохождении сигналов по достаточно большой сети
погрешности гасятся: при больших погрешностях входных сигналов выходные сигналы сети могут иметь
сравнительно малые погрешности. Это
объясняет устойчивость нейронных сетей к шумам и повреждениям.
2. Два базовых подхода к оценкам погрешности
Рассмотрим два
подхода к решению задачи вычисления погрешностей сигналов сети. При первом
подходе (гарантированные интервальные
оценки) вычисляются допустимые интервалы для погрешностей сигналов сети
такие, что погрешность вектора выходных сигналов гарантированно (с вероятностью
1) не превышает заданную. При втором подходе (среднеквадратические оценки погрешностей) вычисляются
среднеквадратические отклонения погрешностей сигналов. При этом часто используется предположение о том, что
погрешности различных сигналов являются независимыми случайными величинами.
Существует
принципиальное различие между этими двумя типами оценок. Гарантированные
интервальные оценки исходят из рассмотрения наихудших возможных случаев, сколь
бы малой не была их вероятность. Поэтому они, как правило, завышают реально
имеющую место ошибку и слишком пессимистичны с практической точки зрения.
Среднеквадратичные оценки, наоборот, стирают возможные большие уклонения и
могут оказаться слишком оптимистичными.
Важное различие
между двумя типами оценок демонстрируют следующие формулы сложения.
1. Формула сложения для интервальных оценок.
Пусть для двух величин x, y
определены гарантированные интервалы значений x=x0±Dx, y=y0±Dy . Тогда для их суммы имеем
гарантированную оценку: x+y= x0+y0 ±(Dx+Dy), то есть Dx+y=Dx+Dy .
2. Формула сложения для среднеквадратичных
уклонений. Пусть для двух независимых
величин x, y определены
среднеквадратичные уклонения sx , sy . Тогда sx+y= (sx2 +sy2)1/2 .
3. Структура сети
Предполагаем,
что сеть имеет слоистую структуру. Это самоограничение позволит несколько
сократить изложение, но не влияет на общность рассмотрения ‑ исследование
любой сети может быть формально сведено к изучению слоистых сетей.
Сеть слоистой
структуры состоит из слоев стандартных нейронов, связанных между собой
синапсами с весами, полученными при обучении. Причем сигналы передаются только
в одном направлении, с предыдущего слоя на следующий. Под стандартным нейроном
[1,2] понимается набор элементов, состоящий из адаптивного сумматора,
нелинейного преобразователя и точки ветвления (рис.1). Точка ветвления – это
элемент, посылающий выходной сигнал нелинейного преобразователя на вход
нескольких стандартных нейронов следующего слоя.
Так как мы имеем
дело с сетями слоистой структуры, состоящими из слоев стандартных нейронов, то
выходные сигналы одного слоя являются входными сигналами другого слоя. В свою
очередь, внутри самого стандартного нейрона выходной сигнал одного элемента
(например, сумматора) является входным сигналом другого элемента (например,
нелинейного преобразователя). Таким образом, можно проследить, начиная с
выходных сигналов сети, от какого элемента сети пришел сигнал к данному
элементу.
Стандартный
нейрон является типичным участком любой нейронной сети. Поэтому достаточно
выяснить, как вычисляются допустимые погрешности для элементов стандартного
нейрона. В результате получим возможность вычислить допустимые погрешности для
любого участка сети, двигаясь по сети от нейрона к нейрону.
4. Метод обратного распространения точности для гарантированных интервальных оценок
Пусть нам заданы
допустимые погрешности вычислений для выходных сигналов сети. Для каждого
элемента решим задачу: определить допустимые погрешности на входах элемента по
заданным максимально допустимым погрешностям на его выходе. Если эту задачу
решить для каждого элемента сети, то можно оценить допустимые погрешности для
всех сигналов, проходящих через сеть, переходя по сети от элемента к элементу в
обратном направлении (от выходов сети к ее входам). Этот процесс мы назовем обратным
распространением точности. В ходе него движение сигналов происходит от
выходов ко входам, сигнал, проходящий по связи в обратном направлении, является
допустимой погрешностью сигнала, проходящего по этой связи в прямом
направлении.
Последним
элементом стандартного нейрона является точка ветвления, поэтому начинаем
рассмотрение метода обратного распространения точности именно с нее.
Точка ветвления
имеет несколько выходов. Пусть для каждого ее выхода задана допустимая
погрешность
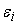 (i - номер выхода). Для того, чтобы удовлетворить всем этим
ограничениям погрешности, необходимо и достаточно, чтобы входной сигнал точки
ветвления имел погрешность
(i - номер выхода). Для того, чтобы удовлетворить всем этим
ограничениям погрешности, необходимо и достаточно, чтобы входной сигнал точки
ветвления имел погрешность
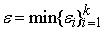 . Таким образом, при обратном распространении точности тока
ветвления заменяется на двойственный элемент, выбирающий из поступающих
сигналов . Таким образом, при обратном распространении точности тока
ветвления заменяется на двойственный элемент, выбирающий из поступающих
сигналов
 (т.е. погрешностей)
минимальный.
(т.е. погрешностей)
минимальный.
Следующим
элементом стандартного нейрона является нелинейный преобразователь. Пусть
входной сигнал нелинейного преобразователя равен
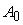 , ,
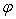 – его функция
активации,
– его функция
активации,
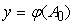 – выходной сигнал и
– выходной сигнал и
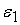 – допустимая
погрешность выходного сигнала. Вычислим максимальную погрешность
– допустимая
погрешность выходного сигнала. Вычислим максимальную погрешность
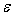 входного сигнала
нелинейного преобразователя, то есть найдем отрезок
входного сигнала
нелинейного преобразователя, то есть найдем отрезок
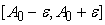 такой, что для любого
такой, что для любого
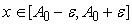
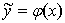 отличается от
отличается от
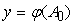 не более, чем на
не более, чем на
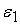 : :
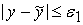 . .
Ввиду
непрерывности и дифференцируемости функции активации нелинейного
преобразователя очевидно, что
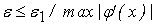 , где , где
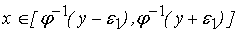 . .
Пойдем
традиционным путем, оценивая допустимую погрешность в линейном приближении:
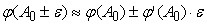 . По условию . По условию
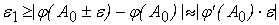 . .
Пользуясь этим
неравенством, подберем
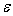 следующим образом:
следующим образом:
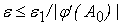 . В этом случае формула для вычисления допустимой погрешности
более простая, но менее точная. . В этом случае формула для вычисления допустимой погрешности
более простая, но менее точная.
Получили
погрешность, допустимую для входного сигнала нелинейного преобразователя,
которая одновременно является допустимой погрешностью для выходного сигнала
сумматора. Аналогично можем вычислить погрешность входного сигнала нелинейного
преобразователя любого стандартного нейрона, если известна погрешность его
выходного сигнала.
Двойственный к
нелинейному преобразователю элемент ‑ просто линейная связь! Ее вес равен
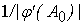 для линейного
приближения в формуле ошибки или
для линейного
приближения в формуле ошибки или
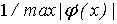 ‑ в более общем случае (в последней формуле максимум
берется по отрезку
‑ в более общем случае (в последней формуле максимум
берется по отрезку
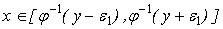 ‑ так что
линейность здесь уже кажущаяся).
‑ так что
линейность здесь уже кажущаяся).
Перейдем к
следующему элементу стандартного нейрона – адаптивному сумматору с
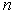 синапсами,
являющимися его входами. Адаптивный сумматор – это сумматор, в котором входные
сигналы
синапсами,
являющимися его входами. Адаптивный сумматор – это сумматор, в котором входные
сигналы
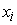 суммируются с весами
суммируются с весами
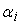 . .
Каждый вход
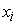 сумматора
сумматора
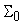 имеет некоторую погрешность
имеет некоторую погрешность
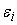 , которая вносит свой вклад в допустимую погрешность
выходного сигнала сумматора. Эти погрешности могут иметь различные величины в
зависимости от того, какой способ распределения допустимой погрешности
выходного сигнала по входам сумматора мы выберем. Погрешности по входам сумматора могут распределяться равномерно,
пропорционально и приоритетно. , которая вносит свой вклад в допустимую погрешность
выходного сигнала сумматора. Эти погрешности могут иметь различные величины в
зависимости от того, какой способ распределения допустимой погрешности
выходного сигнала по входам сумматора мы выберем. Погрешности по входам сумматора могут распределяться равномерно,
пропорционально и приоритетно.
Рассмотрим
сначала равномерное распределение. Для этого полагаем, что на всех входах
погрешности равны между собой
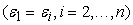 .Пусть .Пусть
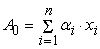 – выходной сигнал
сумматора без погрешностей. Тогда
– выходной сигнал
сумматора без погрешностей. Тогда
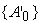 – множество выходных
сигналов сумматора, получающихся, когда вектор входных сигналов сумматора
пробегает вершины
– множество выходных
сигналов сумматора, получающихся, когда вектор входных сигналов сумматора
пробегает вершины
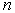 -мерного куба с центром в точке
-мерного куба с центром в точке
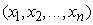 и ребром длины
и ребром длины
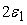 : :
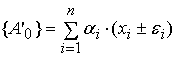 =
=
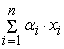 +
+
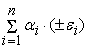 =
=
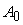 +
+
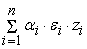 , где , где
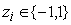 . Нам требуется, чтобы все множество значений . Нам требуется, чтобы все множество значений
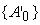 попало в интервал
попало в интервал
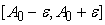 . Для этого необходимо, чтобы . Для этого необходимо, чтобы
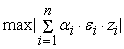 =
=
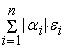
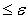 , где максимум берется по всем , где максимум берется по всем
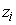 . Из этого неравенства и сделанного выше предположения о . Из этого неравенства и сделанного выше предположения о
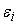 получаем требуемую
оценку для равномерного распределения
получаем требуемую
оценку для равномерного распределения
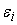 по входам сумматора:
по входам сумматора:
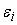
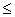
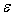 /
/
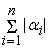 . .
При
пропорциональном распределении погрешностей допустимая погрешность выходного
сигнала сумматора делится сначала на число входов, а затем для каждого входа
делится на соответствующий вес синапса. То есть погрешности распределяются
пропорционально весам соответствующих синапсов. Формула расчета допустимой
погрешности для каждого входа сумматора имеет вид:
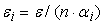 , где , где
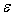 – допустимая
погрешность выходного сигнала сумматора,
– допустимая
погрешность выходного сигнала сумматора,
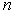 – число входов
сумматора,
– число входов
сумматора,
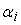 – веса синапсов соответствующих входов сумматора.
– веса синапсов соответствующих входов сумматора.
При приоритетном
распределении погрешностей сначала назначаются погрешности для тех входов,
которые наиболее значимы по какому-либо признаку, а затем оставшуюся часть
допустимой погрешности выходного
сигнала сумматора распределяют между оставшимися входами равномерно или
пропорционально.
Аналогично можно
вычислить допустимые погрешности для входных сигналов сумматора любого
стандартного нейрона, если известны погрешности для выходного сигнала
сумматора.
Для адаптивного
сумматора можно вычислять как допустимые погрешности входных сигналов
сумматора, так и допустимые погрешности весов синапсов. Для вычисления
допустимых погрешностей весов синапсов также можно использовать равномерное,
пропорциональное и приоритетное распределение погрешностей. При равномерном
распределении допустимые погрешности для весов синапсов вычисляются по формуле:
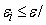
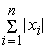 , где , где
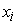 – входные сигналы
сумматора.
– входные сигналы
сумматора.
При
пропорциональном распределении допустимые погрешности для весов синапсов
вычисляются по формуле:
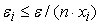 , где , где
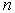 – число входов
сумматора,
– число входов
сумматора,
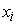 – входные сигналы
сумматора.
– входные сигналы
сумматора.
При приоритетном
распределении сначала назначаются допустимые погрешности для тех весов
синапсов, которые наиболее значимы по какому-либо признаку, а затем оставшуюся
часть допустимой погрешности для выходного сигнала сумматора распределяют между
оставшимися весами синапсов равномерно или пропорционально.
При обратном
распространении точности имеет место специфическая двойственность ‑
элементы сети заменяются на двойственные им. Однако, эта двойственность
отличается от той, с которой мы встречаемся при изучении обратного
распространения ошибки для вычисления градиентов функции оценки. Так, если в
обычном обратном распространении двойственным элементом к точке ветвления
является простой сумматор, то при обратном распространении точности вместо
него, как было показано, появляется
элемент, вычисляющий минимум приходящих на него сигналов. Нелинейный
преобразователь при обратном распространении точности заменяется двойственным
ему элементом, умножающим сигнал на число. Но если при обратном распространении
ошибки множителем является значение градиента, то в нашем случае сигнал
умножается на величину обратную производной от входного сигнала нелинейного
преобразователя. Адаптивный сумматор также заменяется двойственным ему
элементом. Этот элемент является своеобразной точкой ветвления. Но, в отличии
от простой точки ветвления, он сначала преобразует приходящий к нему сигнал в
соответствии с выбранным распределением погрешностей по входам адаптивного
сумматора, а затем передает полученные сигналы дальше.
Теперь мы знаем,
каким образом вычислять гарантированную интервальную оценку погрешности для
любого элемента стандартного нейрона методом обратного распространения
точности.
1) Точка
ветвления. Если допустимые погрешности выходных сигналов точки
ветвления равны
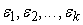 , то в качестве погрешности входного сигнала точки ветвления выбирается , то в качестве погрешности входного сигнала точки ветвления выбирается
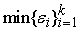 (рис.2).
(рис.2).
2) Нелинейный
преобразователь. Пусть при прямом функционировании входной сигнал
нелинейного преобразователя равен
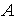 , его выходной сигнал равен , его выходной сигнал равен
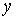 и нелинейный
преобразователь имеет функцию активации
и нелинейный
преобразователь имеет функцию активации
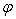 . Если допустимая погрешность выходного сигнала нелинейного
преобразователя равняется . Если допустимая погрешность выходного сигнала нелинейного
преобразователя равняется
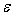 , то погрешность его входного сигнала не должна превышать , то погрешность его входного сигнала не должна превышать
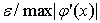 , где , где
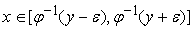 или в линейном
приближении
или в линейном
приближении
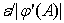 (рис.3).
(рис.3).
3) Адаптивный
сумматор. Если при обратном распространении допустимая погрешность выходного
сигнала адаптивного сумматора равняется
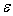 , то погрешность каждого входа сумматора не должна превышать , то погрешность каждого входа сумматора не должна превышать
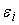 , где , где
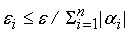 для равномерного
распределения и
для равномерного
распределения и
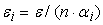 для пропорционального
распределения (рис.4).
для пропорционального
распределения (рис.4).
Зная, как
вычисляются допустимые погрешности для всех элементов стандартного нейрона,
можно вычислить допустимые погрешности сигналов для всей сети. Рассмотрим
участок сети, состоящий из сумматора
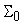 и нелинейного
преобразователя, результатом работы которого является выходной сигнал
и нелинейного
преобразователя, результатом работы которого является выходной сигнал
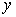 , а также из сумматоров , а также из сумматоров
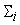 и нелинейных
преобразователей, выходные сигналы которых являются входными сигналами
сумматора
и нелинейных
преобразователей, выходные сигналы которых являются входными сигналами
сумматора
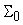 (рис.5). То есть мы
рассматриваем два последних слоя нейронной сети, состоящие из стандартных
нейронов.
(рис.5). То есть мы
рассматриваем два последних слоя нейронной сети, состоящие из стандартных
нейронов.
Если заданы
допустимые погрешности для выходных сигналов сети, можно вычислить допустимые
погрешности для последнего слоя сети. Когда вычислены допустимые погрешности
всех входных сигналов последнего слоя сети, переходим к вычислению допустимых
погрешностей предпоследнего слоя и так далее. Переходя по сети в обратном
направлении от слоя к слою, мы можем вычислить допустимые погрешности всех
сигналов сети, в том числе допустимые погрешности входных сигналов.
Мы рассмотрели,
как изменяются погрешности сигналов при
прохождении через элементы сети. Предположим теперь, что не только сигналы
имеют погрешности, но и все элементы сети передают приходящие к ним сигналы с
некоторыми погрешностями. Пусть собственные
погрешности элементов известны и фиксированы. Выясним, как влияют собственные
погрешности элементов на погрешности сигналов.
Bыясним, как
действуют элементы сети, имеющие собственные погрешности, при прямой работе
сети.
Точка ветвления
может либо вообще не иметь погрешности, либо она имеет собственную погрешность
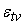 . В последнем случае сигнал . В последнем случае сигнал
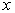 при прохождении через
точку ветвления будет изменяться, оставаясь в интервале
при прохождении через
точку ветвления будет изменяться, оставаясь в интервале
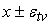 (рис.6).
(рис.6).
Предположим, что
сумматор имеет собственную погрешность
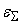 . Тогда возможны следующие варианты: . Тогда возможны следующие варианты:
1) погрешность
прибавляется к выходному сигналу сумматора, т.е. при прохождении сигналов
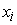 через сумматор
выходной сигнал сумматора будет иметь вид:
через сумматор
выходной сигнал сумматора будет иметь вид:
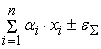 ;
;
2) погрешность
сумматора действует по каждому входу пропорционально
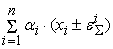 (рис.7).
(рис.7).
Считаем при
этом, что погрешности
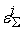 равны между собой и
равны
равны между собой и
равны
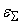 /
/
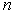 , где , где
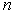 – число входов
сумматора.
– число входов
сумматора.
Пусть
собственная погрешность нелинейного преобразователя равна
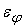 , ,
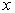 – входной сигнал
нелинейного преобразователя,
– входной сигнал
нелинейного преобразователя,
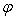 – его функция
активации. Собственная погрешность может добавляться или к входному сигналу
– его функция
активации. Собственная погрешность может добавляться или к входному сигналу
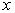 : :
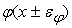 , или к выходному сигналу нелинейного преобразователя: , или к выходному сигналу нелинейного преобразователя:
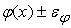 (рис.8).
(рис.8).
Мы выяснили как
вычисляются допустимые погрешности сигналов сети. При этом мы не выделяли особо
тот вклад, который вносят в погрешность сигнала сами элементы. Рассмотрим
теперь, как вычисляются допустимые погрешности сигналов сети при обратном
распространении точности с учетом собственных погрешностей элементов
стандартного нейрона.
Начнем вычисление
допустимых погрешностей сигналов сети с учетом собственных погрешностей
элементов с точки ветвления. Пусть точка ветвления имеет собственную
погрешность
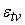 . Предположим, что допустимые погрешности выходных сигналов
точки ветвления равны . Предположим, что допустимые погрешности выходных сигналов
точки ветвления равны
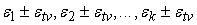 . Для увеличения точности вычислений необходимо накладывать
на допустимые погрешности наиболее жесткие требования. Поэтому в качестве
допустимой погрешности входного сигнала
точки ветвления при обратном распространении следует выбирать
погрешность . Для увеличения точности вычислений необходимо накладывать
на допустимые погрешности наиболее жесткие требования. Поэтому в качестве
допустимой погрешности входного сигнала
точки ветвления при обратном распространении следует выбирать
погрешность
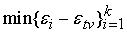 . .
Следующий
элемент стандартного нейрона – нелинейный преобразователь. Если нелинейный
преобразователь имеет собственную погрешность
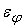 , которая добавляется к его выходному сигналу, и погрешность
его выходного сигнала равняется , которая добавляется к его выходному сигналу, и погрешность
его выходного сигнала равняется
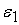 , то допустимая погрешность входного сигнала нелинейного
преобразователя равняется , то допустимая погрешность входного сигнала нелинейного
преобразователя равняется
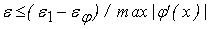 , где , где
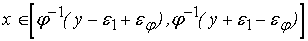 или в линейном
приближении
или в линейном
приближении
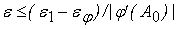 . .
Предположим
теперь, что собственная погрешность нелинейного преобразователя
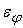 добавляется к его
входному сигналу
добавляется к его
входному сигналу
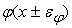 , и при обратном распространении точности погрешность
выходного сигнала нелинейного преобразователя равняется , и при обратном распространении точности погрешность
выходного сигнала нелинейного преобразователя равняется
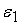 . Рассмотрим наихудший вариант, когда входной сигнал
нелинейного преобразователя находится в интервале . Рассмотрим наихудший вариант, когда входной сигнал
нелинейного преобразователя находится в интервале
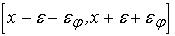 . В этом случае допустимая погрешность входного сигнала
нелинейного преобразователя вычисляется следующим образом: . В этом случае допустимая погрешность входного сигнала
нелинейного преобразователя вычисляется следующим образом:
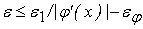 , где , где
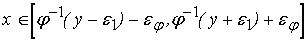 . .
Рассмотрим допустимую
погрешность в линейном приближении:
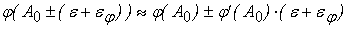 . По условию . По условию
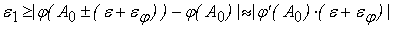 . .
Получаем:
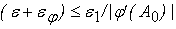 или
или
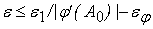 . .
И, наконец,
перейдем к вычислению допустимых погрешностей входных сигналов сумматора.
Рассмотрим вариант, при котором собственная погрешность сумматора
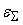 добавляется к его
выходному сигналу, и допустимая
погрешность выходного сигнала сумматора равняется
добавляется к его
выходному сигналу, и допустимая
погрешность выходного сигнала сумматора равняется
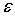 . При обратном распространении точности получаем, что
равномерно, пропорционально и приоритетно по выше полученным формулам
распределяется погрешность . При обратном распространении точности получаем, что
равномерно, пропорционально и приоритетно по выше полученным формулам
распределяется погрешность
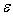 -
-
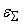 . .
Если же
собственная погрешность сумматора пропорционально распределяется по его входам,
и допустимая погрешность выходного сигнала сумматора равняется
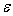 , то допустимые погрешности для входов сумматора вычисляются
следующим образом. Пусть , то допустимые погрешности для входов сумматора вычисляются
следующим образом. Пусть
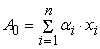 –выходной сигнал
сумматора без погрешностей. Тогда
–выходной сигнал
сумматора без погрешностей. Тогда
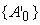 – выходные сигналы
сумматора с учетом собственных погрешностей сумматора
– выходные сигналы
сумматора с учетом собственных погрешностей сумматора
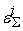 и погрешностей
входных сигналов
и погрешностей
входных сигналов
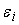 : :
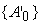 =
=
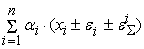 =
=
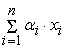 +
+
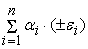 +
+
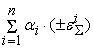 =
=
=
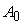 +
+
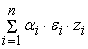 +
+
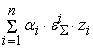 , ,
где
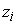 Î{ -1,1 }. Для того, чтобы
все множество
Î{ -1,1 }. Для того, чтобы
все множество
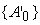 попало в интервал
попало в интервал
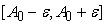 необходимо, чтобы
необходимо, чтобы
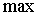 |
|
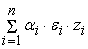 +
+
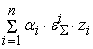 | =
| =
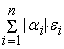 +
+
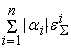
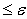 , ,
где максимум
берется по всем
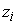 . Из этого неравенства, предполагая что . Из этого неравенства, предполагая что
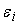 равны между собой,
получаем требуемую оценку для
равны между собой,
получаем требуемую оценку для
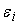 : :
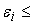 (
(
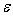 -
-
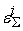
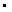
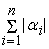 )/
)/
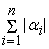 . .
Мы получили
формулы для вычисления допустимых погрешностей сигналов для любого участка сети
с учетом того, что все элементы имеют собственные погрешности, которые вносят
свой вклад в погрешность выходного сигнала этих элементов.
5. Метод обратного распространения точности для анализа реализуемости сетей с
собственными погрешностями элементов
Ранее был
рассмотрен метод обратного распространения точности с учетом собственных
погрешностей элементов сети. Но этот метод может быть использован не для всех
сетей. При применении метода может возникнуть ситуация, когда собственная
погрешность элемента превышает погрешность сигнала, который должен выходить из
этого элемента. Например, если собственная погрешность нейрона
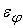 , которая добавляется к выходному сигналу нейрона, превышает
допустимую погрешность его выходного сигнала , которая добавляется к выходному сигналу нейрона, превышает
допустимую погрешность его выходного сигнала
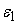 , то по формуле , то по формуле
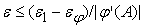 , где , где
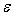 – погрешность входного сигнала нелинейного
преобразователя, получаем отрицательную погрешность. Отрицательные погрешности
в методе обратного распространения точности не имеют смысла, так как мы
рассматриваем допустимую погрешность как величину интервала, в котором может
изменяться погрешность. То же самое можно сказать относительно точки ветвления
и сумматора. В случае получения отрицательной погрешности метод обратного
распространения точности не может применяться. В такой ситуации допустимые
погрешности нужно распределять специальным образом.
– погрешность входного сигнала нелинейного
преобразователя, получаем отрицательную погрешность. Отрицательные погрешности
в методе обратного распространения точности не имеют смысла, так как мы
рассматриваем допустимую погрешность как величину интервала, в котором может
изменяться погрешность. То же самое можно сказать относительно точки ветвления
и сумматора. В случае получения отрицательной погрешности метод обратного
распространения точности не может применяться. В такой ситуации допустимые
погрешности нужно распределять специальным образом.
Рассмотрим
конкретную сеть с заданными собственными погрешностями элементов. Нужно
определить, возможно ли провести вычисления допустимых погрешностей методом
обратного распространения точности с учетом собственных погрешностей элементов
для всех сигналов сети, начиная с выходных
и кончая входными сигналами. Для этого нужно выполнить прямое
функционирование сети с заданными собственными погрешностями элементов и с
точным вектором входных сигналов сети. Если полученный вектор выходных сигналов
при этом будет отличаться от точного вектора выходных сигналов более, чем на
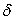 (допустимую погрешность выходных сигналов
сети), то с такими собственными погрешностями элементов для данной сети метод
обратного распространения точности невыполним. В этом случае можно либо
увеличить допустимую погрешность выходных сигналов
(допустимую погрешность выходных сигналов
сети), то с такими собственными погрешностями элементов для данной сети метод
обратного распространения точности невыполним. В этом случае можно либо
увеличить допустимую погрешность выходных сигналов
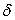 , либо уменьшить собственные погрешности элементов. , либо уменьшить собственные погрешности элементов.
Нам нужно
определить, как вычислять допустимые погрешности сигналов, если это невозможно
сделать методом обратного распространения точности. Выясним, всегда ли возможно распределить их так, чтобы
собственные погрешности элементов не превышали допустимых погрешностей выходных
сигналов этих элементов, и при этом погрешность выходных сигналов сети не превышала
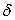 . .
Для точки
ветвления и нелинейного преобразователя формулы вычисления допустимых
погрешностей сигналов методом обратного распространения точности заданы жестко.
Единственным элементом сети, который позволяет влиять на ситуацию, является
сумматор. Для сумматора возможны три варианта распределения допустимых погрешностей
по его входам, в том числе приоритетное. При приоритетном распределении можно
назначать погрешности для тех входов, для которых собственная погрешность
элемента превышает погрешность выходного сигнала.
Если на каком-то
из элементов (нелинейный преобразователь, точка ветвления или сумматор)
собственная погрешность элемента превышает допустимую погрешность его выходного
сигнала, то возвращаемся к тому сумматору, чьим входным сигналом является
выходной сигнал данного элемента. Для этого сумматора распределяем допустимые
погрешности по его входам таким образом, чтобы можно было вычислить допустимую
погрешность входного сигнала того элемента, который нас интересует.
Есть ситуации,
на которые влиять невозможно. К ним относятся следующие:
1) если
собственные погрешности нелинейного преобразователя или сумматора стандартных
нейронов выходного слоя сети превышают погрешности их выходных сигналов;
2) если в
выходном слое сумма с коэффициентами
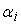 собственных погрешностей элементов
собственных погрешностей элементов
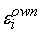 , выходные сигналы которых являются входными сигналами
сумматора, превышает допустимую погрешность , выходные сигналы которых являются входными сигналами
сумматора, превышает допустимую погрешность
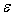 выходного сигнала сумматора:
выходного сигнала сумматора:
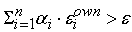 . .
Если собственная
погрешность превышает допустимую
погрешность выходного сигнала у
элемента скрытого или входного слоя, то
можно попытаться распределить
допустимые погрешности так, чтобы продолжить вычисления.
Нам необходимо
оптимально распределить допустимые погрешности по входам сумматора, то есть
распределить их таким образом, чтобы по каждому входу допустимые погрешности
входных сигналов максимально превышали собственные погрешности элементов, чьи
выходные сигналы являются входными сигналами сумматора.
Рассмотрим
участок сети между двумя сумматорами
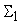 и
и
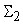 (рис.9). Пусть
(рис.9). Пусть
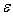 – это погрешность выходного сигнала сумматора
– это погрешность выходного сигнала сумматора
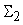 , A – точный
выходной сигнал нелинейного преобразователя. , A – точный
выходной сигнал нелинейного преобразователя.
Предположим
сначала, что собственные погрешности элементов добавляются к выходным сигналам
этих элементов. То есть погрешность входного сигнала нелинейного
преобразователя вычисляется по формуле
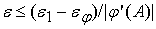 , а для точки ветвления погрешность входного сигнала
определяется как , а для точки ветвления погрешность входного сигнала
определяется как
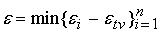 . .
Для каждого
входа сумматора
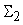 нам необходимо вычислить такие допустимые
погрешности, которые позволили бы провести вычисления допустимых погрешностей
для точки ветвления, нелинейного преобразователя и сумматора
нам необходимо вычислить такие допустимые
погрешности, которые позволили бы провести вычисления допустимых погрешностей
для точки ветвления, нелинейного преобразователя и сумматора
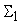 предыдущего слоя. При этом допустимая
погрешность выходного сигнала сумматора
предыдущего слоя. При этом допустимая
погрешность выходного сигнала сумматора
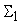 должна превышать его собственную погрешность.
Это гарантирует вычисление допустимых погрешностей для слоя, предшествующего
сумматору
должна превышать его собственную погрешность.
Это гарантирует вычисление допустимых погрешностей для слоя, предшествующего
сумматору
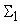 . .
Пусть сумматор
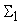 имеет собственную погрешность
имеет собственную погрешность
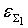 , нелинейный преобразователь имеет собственную погрешность , нелинейный преобразователь имеет собственную погрешность
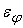 и
и
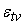 – собственная погрешность точки ветвления.
– собственная погрешность точки ветвления.
Вычислим
погрешность
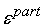 , которая придет к входу сумматора , которая придет к входу сумматора
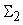 при прямом функционировании сети, начиная от
выходного сигнала сумматора
при прямом функционировании сети, начиная от
выходного сигнала сумматора
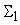 . .
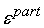 =
=
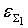
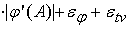 . .
Вычисляем
допустимые погрешности
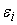 для входов сумматора
для входов сумматора
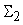 при пропорциональном и равномерном
распределении. Если хотя бы для одного распределения по каждому входу
при пропорциональном и равномерном
распределении. Если хотя бы для одного распределения по каждому входу
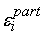 <
<
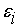 , то можно продолжать вычисления, используя метод обратного
распространения точности с учетом собственных погрешностей элементов сети. Если
же для обоих распределений хотя бы по одному входу , то можно продолжать вычисления, используя метод обратного
распространения точности с учетом собственных погрешностей элементов сети. Если
же для обоих распределений хотя бы по одному входу
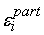 >
>
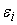 , то необходимо распределять допустимые погрешности по входам
сумматора , то необходимо распределять допустимые погрешности по входам
сумматора
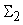 следующим образом.
следующим образом.
Если сумма с
коэффициентами
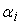 погрешностей
погрешностей
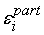 меньше допустимой погрешности выходного сигнала (
меньше допустимой погрешности выходного сигнала (
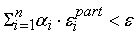 ), то вычисляем разность
), то вычисляем разность
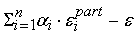 . Оставшуюся часть допустимой погрешности выходного сигнала
сумматора . Оставшуюся часть допустимой погрешности выходного сигнала
сумматора
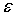 распределяем равномерно по всем входам, чтобы
допустимые погрешности входов превышали погрешности элементов на одну и ту же
величину
распределяем равномерно по всем входам, чтобы
допустимые погрешности входов превышали погрешности элементов на одну и ту же
величину
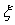 . Тогда
. Тогда
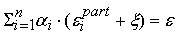
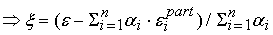 . .
Допустимые
погрешности входных сигналов сумматора будут равны
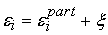 . .
Пусть теперь
собственные погрешности элементов добавляются к их входным сигналам. Допустимая
погрешность входного сигнала нелинейного преобразователя при этом вычисляется
следующим образом:
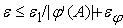 . Собственная погрешность сумматора . Собственная погрешность сумматора
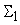 равна
равна
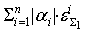 . Допустимая погрешность точки ветвления
вычисляется как было описано выше.
. Допустимая погрешность точки ветвления
вычисляется как было описано выше.
В этом случае погрешности
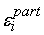 вычисляются по формуле:
вычисляются по формуле:
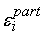 = (
= (
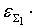
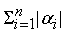 –
–
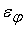 )
)
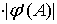 +
+
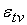 . .
Остальные
вычисления для допустимых погрешностей
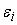 входных сигналов сумматора
входных сигналов сумматора
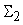 проводятся аналогично.
проводятся аналогично.
Возможен другой
подход. Можно вычислять погрешности
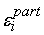 для всей сети сразу. Погрешности
для всей сети сразу. Погрешности
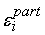 , вычисленные для одного слоя сети, суммируются с
коэффициентами , вычисленные для одного слоя сети, суммируются с
коэффициентами
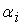 того сумматора, через который они должны
проходить. Полученная погрешность используется дальше для вычисления
погрешности
того сумматора, через который они должны
проходить. Полученная погрешность используется дальше для вычисления
погрешности
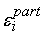 следующего слоя. При обратном прохождении
сети для входов каждого сумматора будет известно, какие погрешности
следующего слоя. При обратном прохождении
сети для входов каждого сумматора будет известно, какие погрешности
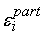 приходят по каждому входу, и как следует
распределять допустимые погрешности сигналов. При этом погрешности
приходят по каждому входу, и как следует
распределять допустимые погрешности сигналов. При этом погрешности
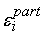 вычисляются один раз и не требуется делать
пересчет.
вычисляются один раз и не требуется делать
пересчет.
Таким образом,
мы рассмотрели как распределяются допустимые погрешности сигналов для сетей с
собственными погрешностями элементов. Используется встречное распространение
погрешностей
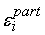 , которые насчитываются при прямом функционировании сети, и
допустимых погрешностей сигналов, которые вычисляются в обратном направлении. , которые насчитываются при прямом функционировании сети, и
допустимых погрешностей сигналов, которые вычисляются в обратном направлении.
6. Метод обратного распространения точности для оценки среднеквадратических отклонений
Рассмотрим
обученную нейросеть с вычисленными весами синапсов
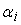 . Считаем, что погрешности входных сигналов, внутренних
сигналов сети и элементов отсутствуют. При векторе входных сигналов . Считаем, что погрешности входных сигналов, внутренних
сигналов сети и элементов отсутствуют. При векторе входных сигналов
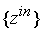 получаем вектор
выходных сигналов
получаем вектор
выходных сигналов
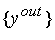 . Вектор . Вектор
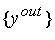 и внутренние сигналы
сети
и внутренние сигналы
сети
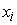 будем считать точным
вектором выходных сигналов и точными сигналами сети.
будем считать точным
вектором выходных сигналов и точными сигналами сети.
Рассмотрим
теперь эту же сеть, но предположим, что все сигналы сети имеют некоторые
погрешности. Пусть
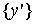 – вектор выходных
сигналов, полученный при том же векторе входных сигналов
– вектор выходных
сигналов, полученный при том же векторе входных сигналов
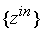 , но с погрешностями внутренних сигналов сети. , но с погрешностями внутренних сигналов сети.
Предполагаем,
что внутри каждого слоя погрешности сигналов
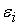
 являются независимыми случайными величинами. Это
предположение позволяет налагать менее жесткие требования при вычислении
погрешностей сигналов.
являются независимыми случайными величинами. Это
предположение позволяет налагать менее жесткие требования при вычислении
погрешностей сигналов.
Пусть нам задана
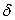 – допустимая
погрешность выходных сигналов сети. То есть вектор
– допустимая
погрешность выходных сигналов сети. То есть вектор
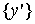 может отличаться от
вектора
может отличаться от
вектора
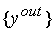 не более, чем на
не более, чем на
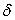 . Будем считать . Будем считать
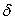 величиной
среднеквадратического отклонения
величиной
среднеквадратического отклонения
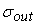 выходных сигналов
сети
выходных сигналов
сети
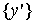 . .
Нам нужно
выяснить, каким образом могут распределяться дисперсии сигналов при заданном
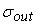 и вычислить
среднеквадратические отклонения
и вычислить
среднеквадратические отклонения
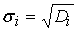 для всех сигналов
сети такие, чтобы среднеквадратическое отклонение вектора выходных сигналов
для всех сигналов
сети такие, чтобы среднеквадратическое отклонение вектора выходных сигналов
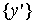 равнялось
равнялось
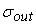 . .
Зная
среднеквадратическое отклонение выходных сигналов, можем вычислить дисперсию
выходных сигналов
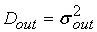 , а затем, переходя от элемента к элементу в обратном
порядке, вычислим дисперсии , а затем, переходя от элемента к элементу в обратном
порядке, вычислим дисперсии
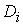 и
среднеквадратические отклонения
и
среднеквадратические отклонения
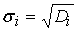 для всех сигналов
сети.
для всех сигналов
сети.
Типичным
участком сети является стандартный нейрон. Из стандартных нейронов состоит
любая нейронная сеть. Поэтому нам достаточно определить, как вычисляются
среднеквадратические отклонения
сигналов для элементов стандартного нейрона. Тогда мы будем иметь
возможность вычислить среднеквадратические отклонения для любого участка сети.
Выясним, как
вычисляются среднеквадратические отклонения для входных сигналов точки
ветвления, нелинейного преобразователя и
сумматора, если нам будут известны среднеквадратические отклонения
выходных сигналов этих элементов.
Если дисперсии
выходных сигналов точки ветвления
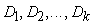 при обратном
распространении не равны между собой, то в качестве дисперсии входного сигнала
точки ветвления выбирается
при обратном
распространении не равны между собой, то в качестве дисперсии входного сигнала
точки ветвления выбирается
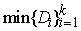 . .
Пусть
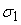 –
среднеквадратическое отклонение погрешности выходного сигнала нелинейного
преобразователя. Пусть случайная величина
–
среднеквадратическое отклонение погрешности выходного сигнала нелинейного
преобразователя. Пусть случайная величина
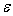 (погрешность входного
сигнала нелинейного преобразователя) имеет некоторую плотность распределения
(погрешность входного
сигнала нелинейного преобразователя) имеет некоторую плотность распределения
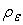 . Считаем, что математическое ожидание погрешности входного
сигнала . Считаем, что математическое ожидание погрешности входного
сигнала
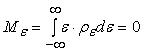 и дисперсия
и дисперсия
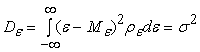 . .
Пусть нелинейный
преобразователь имеет функцию активации
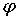 и точный входной
сигнал
и точный входной
сигнал
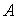 . Рассмотрим линейное приближение функции активации . Рассмотрим линейное приближение функции активации
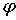 в точке
в точке
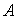 . Линейное приближение имеет вид: . Линейное приближение имеет вид:
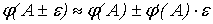 . Найдем математическое ожидание и дисперсию величины . Найдем математическое ожидание и дисперсию величины
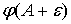 . .
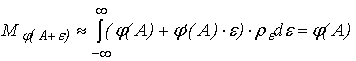 . .
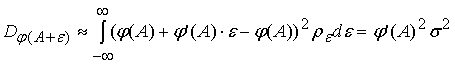 . .
С другой стороны, нам
известно, что дисперсия выходного сигнала нелинейного преобразователя равна
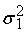 . Отсюда получаем . Отсюда получаем
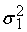 =
=
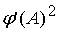
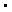
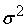
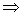
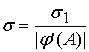 . .
Таким образом,
мы вычислили среднеквадратическое отклонение входного сигнала нелинейного
преобразователя для любого распределения погрешности входного сигнала
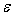 . .
Мы получили
среднеквадратическое отклонение входного сигнала нелинейного преобразователя
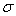 , которое одновременно является среднеквадратическим
отклонением выходного сигнала сумматора с погрешностями входных сигналов , которое одновременно является среднеквадратическим
отклонением выходного сигнала сумматора с погрешностями входных сигналов
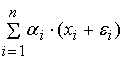 . Погрешность выходного сигнала сумматора равняется . Погрешность выходного сигнала сумматора равняется
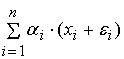 -
-
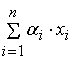 = =
= =
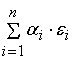 , где , где
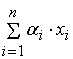 – точный выходной сигнал сумматора.
– точный выходной сигнал сумматора.
Вычислим
среднеквадратические отклонения
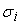 входных сигналов
сумматора. Рассмотрим для этого дисперсию погрешности выходного сигнала
сумматора
входных сигналов
сумматора. Рассмотрим для этого дисперсию погрешности выходного сигнала
сумматора
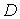 (
(
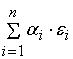 ) =
) =
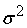 . .
Предположим дополнительно,
что
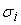 равны между собой.
равны между собой.
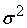 =
=
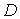 (
(
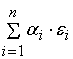 ) =
) =
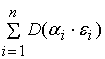 =
=
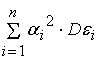 =
=
=
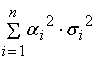
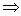
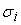 =
=
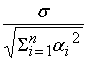 . .
Получили формулу
для равномерного распределения среднеквадратических отклонений
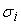 по входам сумматора.
Если в качестве погрешности каждого входа рассматривать не
по входам сумматора.
Если в качестве погрешности каждого входа рассматривать не
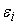 , а , а
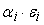 , то получим формулу для пропорционального распределения
среднеквадратических отклонений , то получим формулу для пропорционального распределения
среднеквадратических отклонений
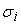 по входам сумматора.
по входам сумматора.
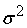 =
=
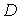 (
(
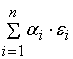 ) =
) =
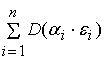 =
=
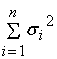
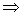
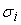 =
=
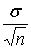 . .
Кроме
равномерного и пропорционального распределения среднеквадратических отклонений
погрешностей по входам сумматора, может быть использовано приоритетное
распределение среднеквадратических отклонений. При этом сначала назначаются
среднеквадратические отклонения погрешностей для тех входов сумматора, которые
наиболее значимы по какому-либо признаку, а затем оставшаяся часть
среднеквадратического отклонения погрешности выходного сигнала сумматора
распределяется по остальным входам равномерно или пропорционально.
Мы рассмотрели,
как изменяются погрешности сигналов при
прохождении через элементы сети. Предположим теперь, что не только сигналы
имеют погрешности, но и все элементы сети передают приходящие к ним сигналы с
некоторыми погрешностями. Пусть среднеквадратические отклонения погрешностей
элементов известны и фиксированы. Выясним, как влияют собственные погрешности
элементов на погрешности сигналов.
Вычислим
среднеквадратические отклонения входных сигналов точки ветвления, нелинейного
преобразователя и сумматора, если известны среднеквадратические отклонения
выходных сигналов и собственные погрешности этих элементов.
Пусть точка
ветвления имеет собственную погрешность
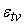 и
среднеквадратическое отклонение собственной погрешности равно
и
среднеквадратическое отклонение собственной погрешности равно
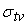 . Собственная погрешность . Собственная погрешность
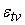 добавляется к каждому
сигналу, выходящему из точки ветвления.
добавляется к каждому
сигналу, выходящему из точки ветвления.
Если при
обратном распространении получаем дисперсии выходных сигналов точки ветвления
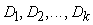 не равные между
собой, то в качестве дисперсии входного сигнала точки ветвления, с учетом
собственной погрешности, выбирается
не равные между
собой, то в качестве дисперсии входного сигнала точки ветвления, с учетом
собственной погрешности, выбирается
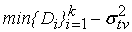 . .
Пусть
среднеквадратическое отклонение собственной погрешности нелинейного
преобразователя равно
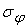 , а среднеквадратическое отклонение выходного сигнала
нелинейного преобразователя равно , а среднеквадратическое отклонение выходного сигнала
нелинейного преобразователя равно
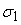 . Собственная погрешность нелинейного преобразователя . Собственная погрешность нелинейного преобразователя
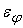 может добавляться
либо к результату работы нелинейного преобразователя:
может добавляться
либо к результату работы нелинейного преобразователя:
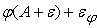 , либо к входному сигналу нелинейного преобразователя: , либо к входному сигналу нелинейного преобразователя:
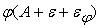 . .
Рассмотрим оба варианта.
Пусть
погрешность
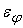 добавляется к
результату работы нелинейного преобразователя. Рассмотрим дисперсию
добавляется к
результату работы нелинейного преобразователя. Рассмотрим дисперсию
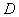 (
(
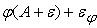 ) =
) =
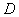 (
(
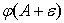 ) +
) +
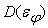 =
=
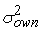 +
+
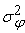 =
=
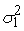 . .
Отсюда получаем, что
дисперсия непосредственно выходного сигнала нелинейного преобразователя равна
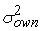 =
=
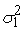 -
-
 . .
Среднеквадратическое
отклонение для входного сигнала нелинейного преобразователя вычисляется как
указано выше. В качестве дисперсии выходного сигнала в формуле используется
вычисленная дисперсия
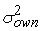 =
=
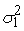 -
-
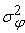 . Среднеквадратическое отклонение погрешности входного
сигнала нелинейного преобразователя будет равняться . Среднеквадратическое отклонение погрешности входного
сигнала нелинейного преобразователя будет равняться
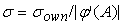 . .
Пусть теперь
собственная погрешность нелинейного преобразователя добавляется к его входному
сигналу:
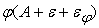 .В этом случае погрешность входного сигнала имеет
математическое ожидание .В этом случае погрешность входного сигнала имеет
математическое ожидание
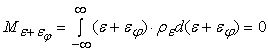 и дисперсию
и дисперсию
 . .
Вычислим
математическое ожидание и дисперсию выходного сигнала нелинейного
преобразователя, рассматривая линейное приближение
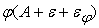 . .
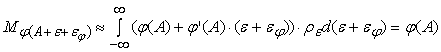 . .
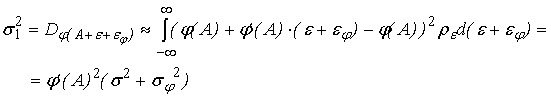 Отсюда получаем
Отсюда получаем
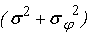 =
=
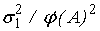
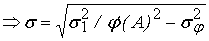 . .
Перейдем к
вычислению среднеквадратических отклонений входных сигналов сумматора. Пусть
среднеквадратическое отклонение выходного сигнала сумматора равно
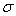 , собственное среднеквадратическое отклонение погрешности
сумматора равно , собственное среднеквадратическое отклонение погрешности
сумматора равно
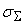 . .
Собственная
погрешность сумматора может добавляться либо к выходному сигналу сумматора:
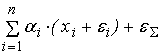 , либо к каждому входу сумматора: , либо к каждому входу сумматора:
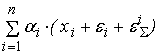 , где , где
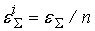 . .
Пусть
собственная погрешность добавляется к выходному сигналу сумматора. Вычислим
среднеквадратическое отклонение погрешностей для входных сигналов сумматора.
Рассмотрим для этого дисперсию
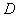 (
(
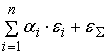 )=
)=
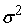 . .
Для равномерного
распределения среднеквадратических отклонений предполагаем, что
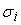 равны между собой.
равны между собой.
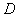 (
(
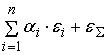 ) =
) =
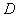 (
(
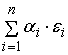 ) +
) +
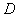 (
(
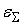 ) =
) =
=
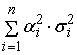 +
+
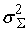
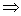
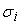 =
=
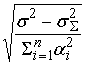 . .
Если будем
рассматривать пропорциональное распределение среднеквадратических отклонений
входных сигналов сумматора, то получим
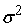 =
=
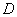 (
(
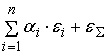 ) =
) =
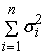 +
+
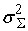
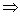
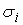 =
=
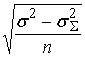 . .
Пусть теперь
собственное среднеквадратическое отклонение сумматора добавляется к каждому
входу сумматора:
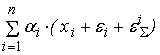 . .
Вычислим
среднеквадратическое отклонение погрешностей для входных сигналов сумматора.
Рассмотрим для этого дисперсию
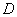 (
(
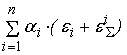 ) =
) =
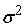 . .
Для равномерного
распределения среднеквадратических отклонений предполагаем, что
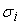 равны между собой.
равны между собой.
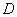 (
(
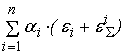 ) =
) =
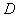 (
(
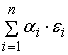 ) +
) +
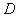 (
(
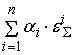 ) =
) =
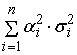 +
+
+
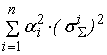
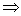
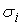 =
=
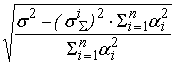 . .
Если будем
рассматривать пропорциональное распределение среднеквадратических отклонений
входных сигналов сумматора, то получим
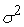 =
=
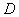 (
(
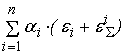 ) =
) =
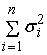 +
+
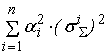
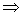
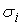 =
=
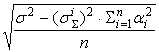
Зная, как
вычисляются среднеквадратические отклонения погрешностей для всех элементов
стандартного нейрона, можно вычислить среднеквадратические отклонения
погрешностей сигналов для всей сети. Если заданы среднеквадратические
отклонения погрешностей для выходных сигналов сети, можно вычислить
среднеквадратические отклонения погрешностей для последнего слоя сети. Когда
вычислены среднеквадратические отклонения погрешностей всех входных сигналов
последнего слоя сети, переходим к вычислению среднеквадратических отклонений
погрешностей предпоследнего слоя и так далее.
Рассмотрим
пример на рис.10. Пусть дана сеть с тремя нейронами входного слоя, двумя
нейронами скрытого слоя и одним выходным нейроном. На рисунке показаны сигналы,
проходящие по сети при данном векторе входных сигналов, и веса связей. В данном
примере элементы сети не имеют собственных погрешностей. Характеристическая
функция нелинейных преобразователей имеет вид:
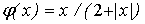 , где , где
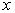 – входной сигнал
нелинейного преобразователя. Среднеквадратическое отклонение вектора выходных
сигналов сети
– входной сигнал
нелинейного преобразователя. Среднеквадратическое отклонение вектора выходных
сигналов сети
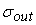 равняется 0.01.
Среднеквадратические отклонения погрешностей по входам сумматора вычисляются с
использованием формулы для равномерного распределения среднеквадратических
отклонений.
равняется 0.01.
Среднеквадратические отклонения погрешностей по входам сумматора вычисляются с
использованием формулы для равномерного распределения среднеквадратических
отклонений.
Вычислим среднеквадратические отклонения для всех сигналов
сети при данном векторе входных сигналов. Все вычисленные значения в этом
примере округляются до двух знаков после запятой. На рис.11 показаны
вычисленные среднеквадратические отклонения для данного примера.
Зная, как
вычисляются среднеквадратические отклонения погрешностей для всех элементов
стандартного нейрона, можно вычислить среднеквадратические отклонения
погрешностей сигналов для всей сети. Если заданы среднеквадратические
отклонения погрешностей для выходных сигналов сети, можно вычислить среднеквадратические
отклонения погрешностей для последнего слоя сети. Когда вычислены
среднеквадратические отклонения погрешностей всех входных сигналов последнего
слоя сети, переходим к вычислению среднеквадратических отклонений погрешностей
предпоследнего слоя и так далее.
Рассмотрим
пример на рис.10. Пусть дана сеть с тремя нейронами входного слоя, двумя
нейронами скрытого слоя и одним выходным нейроном. На рисунке показаны сигналы,
проходящие по сети при данном векторе входных сигналов, и веса связей. В данном
примере элементы сети не имеют собственных погрешностей. Характеристическая
функция нелинейных преобразователей имеет вид:
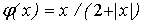 , где , где
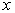 – входной сигнал
нелинейного преобразователя. Среднеквадратическое отклонение вектора выходных
сигналов сети
– входной сигнал
нелинейного преобразователя. Среднеквадратическое отклонение вектора выходных
сигналов сети
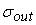 равняется 0.01.
Среднеквадратические отклонения погрешностей по входам сумматора вычисляются с
использованием формулы для равномерного распределения среднеквадратических
отклонений.
равняется 0.01.
Среднеквадратические отклонения погрешностей по входам сумматора вычисляются с
использованием формулы для равномерного распределения среднеквадратических
отклонений.
Вычислим среднеквадратические отклонения для всех сигналов
сети при данном векторе входных сигналов. Все вычисленные значения в этом
примере округляются до двух знаков после запятой. На рис.11 показаны
вычисленные среднеквадратические отклонения для данного примера.
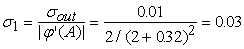 ; ;
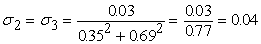 ; ;
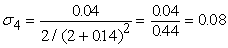 ; ;
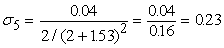 ; ;
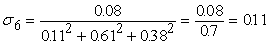 ; ;
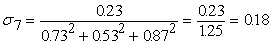 ; ;
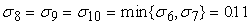 ; ;
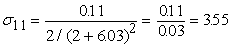 ; ;
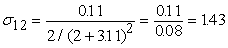 ; ;
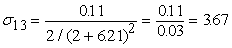 ; ;
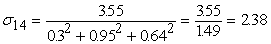 ; ;
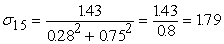 ; ;
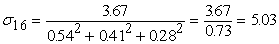 ; ;
Таким образом,
получены формулы для вычисления среднеквадратических отклонений погрешностей
сигналов сети, в предположении, что погрешности являются независимыми
случайными величинами.
7. Анализ реализуемости сетей с собственными погрешностями элементов методом обратного
распространения точности для оценки среднеквадратических отклонений
Все изложенные
выше соображения о выполнимости метода обратного распространения точности
справедливы и для метода обратного распространения точности для
среднеквадратических отклонений погрешностей с учетом собственных погрешностей
элементов. Отличие состоит в способе вычисления промежуточных
среднеквадратических отклонений погрешностей.
Как и выше,
рассмотрим участок сети, изображенный на рис.9. Для этого участка нам
необходимо вычислить промежуточное среднеквадратическое отклонение погрешности
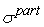 . .
Пусть
собственное среднеквадратическое отклонение погрешности сумматора
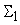 равно
равно
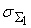 , собственное среднеквадратическое отклонение погрешности
нелинейного преобразователя равно , собственное среднеквадратическое отклонение погрешности
нелинейного преобразователя равно
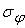 и
и
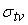 – собственное
среднеквадратическое отклонение погрешности точки ветвления.
– собственное
среднеквадратическое отклонение погрешности точки ветвления.
Рассмотрим
сначала вариант, когда собственные погрешности элементов добавляются к выходным
сигналам этих элементов. В этом случае среднеквадратическое отклонение
погрешности входного сигнала нелинейного преобразователя вычисляется по формуле
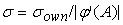 , где , где
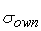 =
=
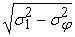 , ,
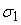 – общая погрешность выходного сигнала нелинейного
преобразователя. Для точки ветвления среднеквадратическое отклонение
погрешности входного сигнала определяется как
– общая погрешность выходного сигнала нелинейного
преобразователя. Для точки ветвления среднеквадратическое отклонение
погрешности входного сигнала определяется как
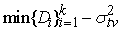 . .
Среднеквадратическое
отклонение погрешности
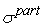 , которое придет к входу сумматора , которое придет к входу сумматора
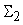 при прямом
функционировании сети, начиная от выходного сигнала сумматора
при прямом
функционировании сети, начиная от выходного сигнала сумматора
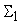 (рис.9), равно
(рис.9), равно
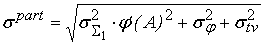 . .
Среднеквадратические
отклонения погрешностей
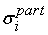 придут к каждому
входу сумматора
придут к каждому
входу сумматора
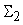 . Если сумма квадратов среднеквадратических отклонений . Если сумма квадратов среднеквадратических отклонений
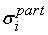 с коэффициентами
с коэффициентами
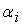 меньше квадрата
среднеквадратического отклонения погрешности выходного сигнала сумматора (
меньше квадрата
среднеквадратического отклонения погрешности выходного сигнала сумматора (
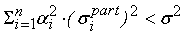 ), то вычисляем разность
), то вычисляем разность
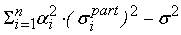 . Оставшуюся часть квадрата среднеквадратического отклонения
погрешности выходного сигнала сумматора . Оставшуюся часть квадрата среднеквадратического отклонения
погрешности выходного сигнала сумматора
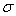 распределяем
равномерно по всем входам, чтобы среднеквадратические отклонения погрешностей
входов превышали собственные среднеквадратические отклонения погрешностей
элементов на одну и ту же величину
распределяем
равномерно по всем входам, чтобы среднеквадратические отклонения погрешностей
входов превышали собственные среднеквадратические отклонения погрешностей
элементов на одну и ту же величину
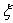 . Тогда получаем следующую формулу . Тогда получаем следующую формулу
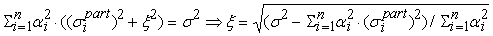 . .
Среднеквадратические
отклонения погрешностей по входам сумматора будут равны
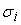 =
=
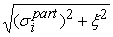 . .
Пусть теперь
собственные погрешности элементов добавляются к входным сигналам этих
элементов. В этом случае среднеквадратическое отклонение погрешности входного
сигнала нелинейного преобразователя вычисляется по формуле
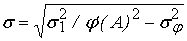 , где , где
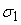 – погрешность
выходного сигнала нелинейного преобразователя. Для точки ветвления
среднеквадратическое отклонение погрешности входного сигнала определяется как
было указано выше.
– погрешность
выходного сигнала нелинейного преобразователя. Для точки ветвления
среднеквадратическое отклонение погрешности входного сигнала определяется как
было указано выше.
Среднеквадратическое
отклонение погрешности
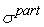 в этом случае равно
в этом случае равно
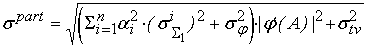 . .
Величины
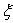 для вычисления
среднеквадратических отклонений погрешностей входных сигналов
для вычисления
среднеквадратических отклонений погрешностей входных сигналов
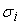 вычисляются как было
показано выше.
вычисляются как было
показано выше.
Промежуточные
среднеквадратические отклонения погрешностей
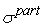 можно вычислять как для участков сети, так и для сети в
целом.
можно вычислять как для участков сети, так и для сети в
целом.
Таким образом,
мы получили формулы для вычисления среднеквадратических отклонений погрешностей
сигналов нейронной сети с собственными погрешностями элементов.
Типы погрешностей
В методе обратного распространения точности
приведены формулы для вычисления погрешностей сигналов сети. Эти формулы рассчитаны
для сигналов, полученных при прямом функционировании сети с одним примером из
обучающей выборки в качестве входных сигналов сети. Вообще говоря, допустимые
погрешности сигналов зависят от вида входных сигналов сети. Исходя из этого,
для метода обратного распространения точности можно выделить четыре типа
допустимых погрешностей:
1) погрешности,
вычисленные для одного примера;
2) погрешности, вычисленные
для всей обучающей выборки;
3) погрешности, вычисленные
для примеров, компоненты которых принадлежат области
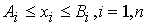 , где , где
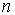 – размерность области,
– размерность области,
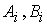 – действительные числа;
– действительные числа;
4) погрешности, вычисленные
для примеров, компоненты которых принадлежат области
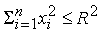 , где R –
действительное число. , где R –
действительное число.
Погрешности первого типа вычисляются по
формулам, описанным в методе обратного распространения точности.
Для того, чтобы вычислить погрешности
второго типа, вычисляем погрешности для каждого примера из обучающей выборки.
Затем в качестве допустимой погрешности для каждого элемента сети выбирается
минимум допустимых погрешностей этого элемента, вычисленных для каждого примера
из обучающей выборки.
Рассмотрим, как вычисляются допустимые
погрешности третьего и четвертого типов. В формулах для вычисления допустимых
погрешностей входной сигнал используется только у нелинейного преобразователя.
Допустимые погрешности остальных элементов сети от входных сигналов не зависят.
Поэтому для вычисления этих типов погрешностей следует выяснить, какие сигналы
будут входными для нелинейных преобразователей, если входные сигналы сети
принадлежат области, которая является прямоугольником или шаром.
Для начала рассмотрим допустимые погрешности
третьего типа, то есть те допустимые погрешности элементов сети, которые
получаются при входных сигналах, принадлежащих прямоугольной области. Нам
известны интервалы, в которых изменяются входные сигналы сети. Требуется
вычислить интервалы для входных сигналов каждого элемента сети. Будем вычислять
их следующим образом. При прохождении интервалов через сумматор концы
интервалов соответствующих входов умножаются на веса синапсов
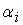 и затем складываются.
Предположим, что функция активации нелинейного преобразователя непрерывна и
монотонна. Тогда в качестве концов интервала его выходного сигнала берутся
значения характеристической функции нелинейного преобразователя от концов
интервала входного сигнала. Точка ветвления посылает приходящий к ней интервал
на входы следующих элементов. Таким образом, для каждого элемента сети мы можем
вычислить интервал, в котором изменяются его входные сигналы. Нас интересуют
интервалы, в которых изменяются входные сигналы нелинейных преобразователей.
Для того, чтобы вычислить допустимые погрешности входного сигнала нелинейного
преобразователя, необходимо вычислить максимум производной функции активации
нелинейного преобразователя на интервале изменения его входных сигналов и затем
разделить на эту величину допустимую погрешность выходного сигнала нелинейного
преобразователя.
и затем складываются.
Предположим, что функция активации нелинейного преобразователя непрерывна и
монотонна. Тогда в качестве концов интервала его выходного сигнала берутся
значения характеристической функции нелинейного преобразователя от концов
интервала входного сигнала. Точка ветвления посылает приходящий к ней интервал
на входы следующих элементов. Таким образом, для каждого элемента сети мы можем
вычислить интервал, в котором изменяются его входные сигналы. Нас интересуют
интервалы, в которых изменяются входные сигналы нелинейных преобразователей.
Для того, чтобы вычислить допустимые погрешности входного сигнала нелинейного
преобразователя, необходимо вычислить максимум производной функции активации
нелинейного преобразователя на интервале изменения его входных сигналов и затем
разделить на эту величину допустимую погрешность выходного сигнала нелинейного
преобразователя.
Таким образом
вычисляются допустимые погрешности сигналов сети для прямоугольной области
входных сигналов сети.
Рассмотрим
пример, в котором будем вычислять погрешности третьего типа. Воспользуемся
нейросетью, изображенной на рис.9. Нейросеть имеет такие же веса синапсов, но
входные сигналы принадлежат прямоугольной области:
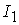 =[-2,6]; =[-2,6];
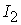 =[3,11]; =[3,11];
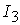 =[1.5,4]; =[1.5,4];
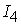 =[2,7]; =[2,7];
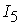 =[4,10]; =[4,10];
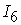 =[-5,5]; =[-5,5];
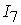 =[1,8]; =[1,8];
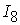 =[-4,6]. =[-4,6].
Сигналы сети изменяются в следующих
интервалах:
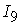 =[-0.6,3.6]; =[-0.6,3.6];
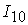 =[2.85,10.45]; =[2.85,10.45];
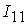 =[0.96,2.56]; =[0.96,2.56];
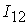 =[0.56,1.96]; =[0.56,1.96];
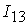 =[3,7.5]; =[3,7.5];
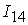 =[-2.7,2.7]; =[-2.7,2.7];
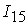 =[0.41,3.28]; =[0.41,3.28];
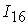 =[-1.12,1.68]; =[-1.12,1.68];
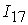 =[3.21,16.61]; =[3.21,16.61];
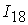 =[3.56,9.46]; =[3.56,9.46];
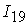 =[-3.41,7.66]; =[-3.41,7.66];
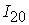 =[0.62,0.89]; =[0.62,0.89];
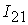 =[0.64,0.83]; =[0.64,0.83];
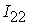 =[-0.63,0.79]; =[-0.63,0.79];
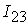 =[0.07,0.1]; =[0.07,0.1];
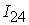 =[0.45,0.65]; =[0.45,0.65];
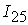 =[0.39,0.51]; =[0.39,0.51];
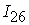 =[0.34,0.44; =[0.34,0.44;
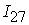 =[-0.2,0.26]; =[-0.2,0.26];
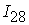 =[-0.55,0.69]; =[-0.55,0.69];
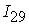 =[0.26,0.86]; =[0.26,0.86];
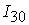 =[0.24,1.78]; =[0.24,1.78];
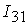 =[0.12,0.3]; =[0.12,0.3];
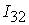 =[0.1,0.47]; =[0.1,0.47];
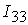 =[0.04,0.1]; =[0.04,0.1];
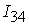 =[0.07,0.32]; =[0.07,0.32];
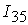 =[0.11,0.42]; =[0.11,0.42];
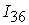 =[0.05,0.17]. =[0.05,0.17].
Мы можем вычислить максимум производной функции активации на
интервале изменения входного сигнала нелинейного преобразователя.
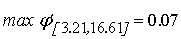 ;
;
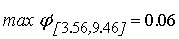 ;
;
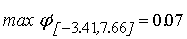 ;
;
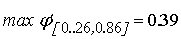 ;
;
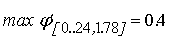 ;
;
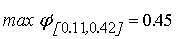 . .
Зная эти
величины, можно вычислить допустимые погрешности третьего типа.
Выясним теперь,
как вычисляются допустимые погрешности сигналов четвертого типа, то есть
погрешности, получающиеся, когда область входных сигналов сети является шаром.
Рассуждения,
приведенные выше для допустимых погрешностей третьего типа, справедливы и для
допустимых погрешностей четвертого типа. Отличие состоит в том, что нам
необходимо "развернуть" шаровую область таким образом, чтобы получить
интервалы, в которых изменяются входные сигналы элементов.
Рассмотрим для
этого квадраты выходных сигналов сумматоров входного слоя сети. Используя
неравенство Коши, получаем
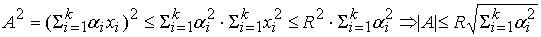 , ,
где
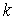 – число входных
сигналов сумматора. Получили интервалы, в которых изменяются выходные сигналы
сумматоров входного слоя нейронной сети. Используя эти интервалы, можем
вычислить интервалы, в которых изменяются входные сигналы элементов сети.
Затем, как уже было описано выше, вычисляем допустимые погрешности входных
сигналов нелинейных преобразователей.
– число входных
сигналов сумматора. Получили интервалы, в которых изменяются выходные сигналы
сумматоров входного слоя нейронной сети. Используя эти интервалы, можем
вычислить интервалы, в которых изменяются входные сигналы элементов сети.
Затем, как уже было описано выше, вычисляем допустимые погрешности входных
сигналов нелинейных преобразователей.
8. Обсуждение
Как метод
обратного распространения точности, так и метод обратного распространения
среднеквадратических отклонений погрешностей можно применять к сетям не только
слоистой структуры, но также к циклическим и полносвязным сетям. Рассматривая
такт функционирования сети как слой, "разворачиваем" циклические и
полносвязные сети в сети слоистой структуры. Вычисляем допустимые погрешности
(среднеквадратические отклонения погрешностей) для сигналов стандартных
нейронов каждого слоя. Затем "сворачиваем" слоистую сеть в исходную.
Так как каждый слой полученной сети на самом деле является тактом
функционирования, то для каждого сигнала сети на разных тактах получаем разные
допустимые погрешности (среднеквадратические отклонения погрешностей). В
качестве допустимой погрешности (среднеквадратического отклонения погрешности)
для каждого сигнала сети выбирается минимум этих величин по всем тактам.
Идея этих
методов возникла при решении задачи бинаризации нейронной сети. Бинаризация
состоит в построении такой сети, которая функционирует так же, как и исходная,
но имеет веса синапсов, равные 0 или 1 (вариант: +1 или ‑1).
Но метод
обратного распространения точности и метод обратного распространения
среднеквадратических отклонений погрешностей сигналов сети интересен не только
и не столько в приложении к задаче бинаризации. Их можно применять при решении
ряда других задач. Например, вычислив допустимые погрешности
(среднеквадратические отклонения погрешностей) для всей сети, можно выяснить, в
каких пределах можно варьировать входные данные и сигналы на любом участке
сети, чтобы вектор выходных сигналов при этом изменился не более, чем на
заданную величину.
Метод обратного
распространения точности для среднеквадратических оценок погрешности позволяет
получать формулы для вычисления погрешностей сигналов сети, налагающие менее
жесткие ограничения на величину погрешностей по сравнению с гарантированными
интервальными оценками погрешностями. Если для гарантированных интервальных
оценок при обратном прохождении слоев допустимые погрешности сигналов
уменьшаются, то для среднеквадратических оценок погрешностей есть ситуации,
когда погрешности увеличиваются от последнего слоя к первому. Если погрешности
сигналов являются независимыми случайными величинами, то, как показано в
примере, даже при больших погрешностях входных сигналов получаются достаточно
точные выходные сигналы.
9. Заключение.
Таким образом,
решение задачи вычисления допустимых погрешностей (среднеквадратических
отклонений погрешностей) для каждого сигнала сети методом обратного
распространения точности удивительно похоже на метод обратного распространения
ошибки, но с другими правилами прохождения элементов. Метод позволяет
формулировать требования к точности вычисления и реализации технических
устройств, если известны требования к точности выходных сигналов сети.
Литература.
- Горбань А.Н. Обучение нейронных сетей. –М.: СП “ПараГраф”, 1990. – 159 с.
- Нейроинформатика и ее приложения // Материалы 3 Всероссийского семинара, 6-8 октября 1995 г. Ч. 1
/Под редакцией А.Н.Горбаня. Отв. за выпуск Г.М.Цибульский; Красноярск: изд.
КГТУ. – 1995. – 229 с.
- Kimura T., Shima T. Synapse weight accuracy of analog neuro chip //
Proceedings of International Joint Conference on Neural Networks. – Japan,
Nagoya, October 25-29, 1993. – Vol.1. – P. 891-894.
- Anguita D., Ridella S., Rovetta S. Limiting the effects of weight errors
in feed forward networks using interval arithmetic // Proceedings of
International Conference on Neural Networks (ICNN’96). – USA, Washington, June
3-6, 1996. – Vol.1. – P. 414-417.
- Edwards P., Murray A. Modelling weight- and input-noise in MLP learning
// Proceedings Of International Conference on Neural Networks (ICNN’96). – USA,
Washington, June 3-6, 1996. – Vol.1. – P. 78-83.
- Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. Новосибирск:
Наука. Сибирская издательская фирма РАН, 1996. – 276 с.
- Боровков А.А. Теория вероятностей. М.: Наука, 1976. – 352 с.
- Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1969.– 400 с.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки