|
Далее мы рассмотрим подробнее способ представления обучающей выборки; виды объектов и способ представления сведений о них; способ сравнения объектов и вычисления степени уверенности отнесения объекта к какому-либо классу.
Принятые обозначения
В данной главе будет использованы некоторые математические понятия и обозначения, требующие предварительного разъяснения.
Выражение:

возвращает первое (сверху вниз) из значений (A, B, C,..., X, Y) у которого соответствующее условие будет истинным. Если ни одно из условий не является истинным, то возвращается то значение, для которого условий не указано (Z, в нашем примере).
Выражение:

показывает, что перед выполнением функции 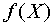 необходимо выполнить действия с 1 по N в порядке следования их номеров. Результатом данного выражения будет результат функции необходимо выполнить действия с 1 по N в порядке следования их номеров. Результатом данного выражения будет результат функции 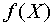 . .
Выражение  показывает, что некоторой переменной показывает, что некоторой переменной  присваивается некоторое значение присваивается некоторое значение 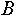 . .
Знак равенства (=) будем использовать лишь для проверки равенства левого и правого значений (например, выражение 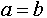 будет истинным, если будет истинным, если 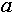 равно равно 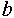 , и ложным в противном случае). , и ложным в противном случае).
Выражение 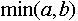 эквивалентно эквивалентно 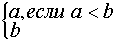
Выражение 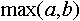 эквивалентно эквивалентно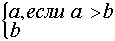
Выражение 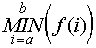 возвращает минимальное значение возвращает минимальное значение 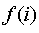 при целом при целом 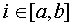 . .
Выражение 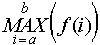 возвращает максимальное значение возвращает максимальное значение 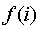 при целом при целом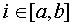 . .
Выражение 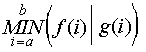 возвращает значение возвращает значение 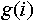 при целом при целом 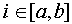 и и 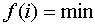 . .
Выражение 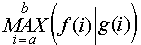 возвращает значение возвращает значение 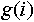 при целом при целом 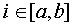 и и 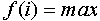 . .
Понятие индексированного множества
Индексированно множество – это множество, каждый объект которого имеет уникальную метку, отличную от меток других объектов данного множества. Условимся, что функция 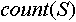 возвращает количество объектов, содержащихся в данном индексированном множестве возвращает количество объектов, содержащихся в данном индексированном множестве 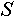 . Индекс объекта данного индексированного множества . Индекс объекта данного индексированного множества 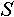 - это метка, представляющая собой целое число в интервале от 1 до - это метка, представляющая собой целое число в интервале от 1 до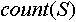 включительно. Один и тот же объект может иметь в разных множества разные индексы. Условимся, что функция включительно. Один и тот же объект может иметь в разных множества разные индексы. Условимся, что функция 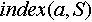 возвращает индекс объекта возвращает индекс объекта 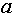 в индексированном множестве в индексированном множестве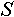 . Условием применения данной функции является условие обязательного наличия данного объекта в данном множестве. . Условием применения данной функции является условие обязательного наличия данного объекта в данном множестве.
Рассмотрим действия с индексированными множествами:
- Обращение к объекту с индексом
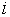 , индексированного множества , индексированного множества 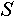 будем записывать как будем записывать как 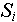
- Создание индексированного множества будем записывать как
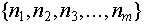 , где , где 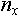 - один из объектов, входящий во вновь создаваемое индексированное множество. Индексы объектам будут присвоены в зависимости от порядка их следования в записи - первый объект получит индекс равный 1, второй объект - индекс равный 2, третий - 3 и т. д. Например создание индексированного множества - один из объектов, входящий во вновь создаваемое индексированное множество. Индексы объектам будут присвоены в зависимости от порядка их следования в записи - первый объект получит индекс равный 1, второй объект - индекс равный 2, третий - 3 и т. д. Например создание индексированного множества 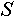 состоящего из объектов состоящего из объектов  можно записать указав: можно записать указав: 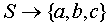 , тогда , тогда 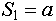 , , 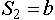 , , 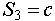 . Создание пустого индексированного множества будем обозначать как . Создание пустого индексированного множества будем обозначать как  . .
- Сравнение индексированных множеств. Два индексированных множества
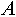 и и 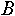 будем считать равными друг другу, если выполняются следующие условия: будем считать равными друг другу, если выполняются следующие условия:
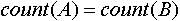 и и
при любом целом 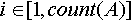 объект объект 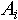 будет являться абсолютно идентичной копией будет являться абсолютно идентичной копией 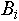 . .
Таким образом, например:
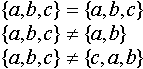
- Объединение индексированных множеств
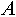 и и 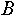 будем записывать как будем записывать как 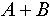 . Индексированное множество . Индексированное множество 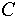 будем считать равным объединению индексированных множеств будем считать равным объединению индексированных множеств 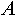 и и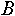 , если: , если:
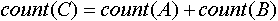 и и
при любом целом 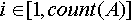 будет верно будет верно 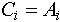 и и
при любом целом 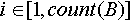 будет верно будет верно 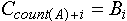 . .
Например:
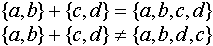
- Исключение множества
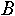 из индексированного множества из индексированного множества 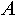 будем записывать как будем записывать как 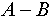 . Индексированное множество . Индексированное множество 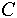 будет равно результату будет равно результату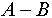 , если , если 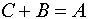 . .
- Построение из индексированного множества
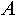 индексированного подмножества можно записать, указав индексированного подмножества можно записать, указав 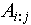 . Индексированное множество . Индексированное множество 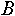 будет равно будет равно 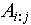 , если при любом , если при любом 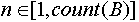 будут выполняться следующие условия: будут выполняться следующие условия:
 и и
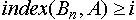 и и
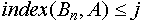 . .
- Имена объектов индексированного множества. Имя данного объекта в данном индексированном множестве - это некоторая константа, хранящая индекс данного объекта в данном множестве. Имена применяются для мнемонического обозначения некоторых объектов. Для устранения путаницы не будем использовать более одного имени данного объекта в данном множестве. При использовании имен объектов можно не указывать предварительно конкретное, числовое значение имени, как константы.
Запись вида 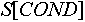 показывает, что мы обращаемся в индексированном множестве показывает, что мы обращаемся в индексированном множестве 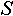 к объекту, поименованному в этом множестве как к объекту, поименованному в этом множестве как 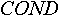 . Это, также показывает, что для индексированного множества . Это, также показывает, что для индексированного множества 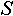 определена константа определена константа 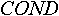 , хранящая индекс данного объекта в данном индексированном множестве. В случае, если ни один объект множества , хранящая индекс данного объекта в данном индексированном множестве. В случае, если ни один объект множества 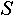 не поименован как не поименован как 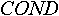 , то результатом обращения будет пустое множество. , то результатом обращения будет пустое множество.
Присвоение имени, например 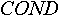 , некоторому объекту , некоторому объекту 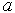 в индексированном множестве в индексированном множестве 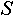 будем записывать как будем записывать как 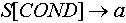 . Если, до присвоения имени, объект не входил в данное индексированное множество, то он будет включен в него. . Если, до присвоения имени, объект не входил в данное индексированное множество, то он будет включен в него.
- Вектора, матрицы, вложенные индексированные множества. Будем называть вектором - индексированное множество чисел; матрицей - индексированное множество матриц или векторов. При обращении к элементам индексированных множеств, которые (множества) сами являются элементами некоторого другого индексированного множества, сначала будем указывать индекса множеств-элементов, а затем - индекса соответствующих элементов вложенных множеств. Например, запись
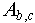 показывает обращение к элементу с индексом показывает обращение к элементу с индексом  в индексированном множестве, являющемся элементом с индексом в индексированном множестве, являющемся элементом с индексом  в индексированном множестве в индексированном множестве 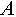 . .
Разобьем обучающую выборку на подмножества, в каждое из которых входят лишь сведения о объектах одного класса. В рамках данной работы мы будем представлять обучающую выборку в виде индексированного множества CLASSES, элементы которого - индексированные множества, состоящие из сведений о объектах одного класса обучающей выборки.
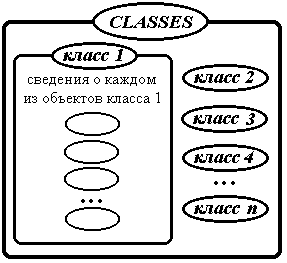
Рисунок 2. Представление обучающей выборки
В данной работе мы будем сведения о каждом из объектов предметной области хранить в отдельном индексированном множестве. В дальнейшем, говоря "опишем для объекта А элемент сведений В" мы будем подразумевать, что в индексированном множестве, хранящем сведения о объекте А, существует элемент, поименованный как В.
Каждый из объектов обладает некоторым набором признаков, свойств. Например, признаками объекта "комната" могут быть "площадь", "освещенность", "температура воздуха", "мебель" и т. п.. Каждый из признаков объекта имеет определенное значение, выражение. Если значение признака можно выразить одним числом, то будем называть такой признак простым, иначе - сложным. Простыми признаками объекта "комната", в нашем примере, являются "площадь", "освещенность", "температура воздуха", так как они могут быть выражены числом квадратных метров, свечей и градусов Цельсия, соответственно; признак "мебель" не является простым, так как он не может быть выражен одном числом.
Для каждого объекта опишем индексированное множество С (от англ. components - компоненты), элементами которого будут являться описания каждого из признаков - индексированные множества, каждое из которых хранит сведения о одном из признаков данного объекта. В дальнейшем, говоря "опишем для признака А элемент сведений В" мы будем подразумевать, что в индексированном множестве, хранящем сведения о признаке А, существует элемент, поименованный как В.
Значение признака может принадлежать каким-либо классам значений. Например, значение признака "температура воздуха" объекта "комната" можно классифицировать как "холодно", "нормально", "жарко". Для каждого класса значений признака можно описать функцию принадлежности значения данного признака данному классу значений. Функция принадлежности возвращает число в интервале от 0 до 1 включительно, показывающее степень уверенности в том, что значение данного признака относится к данному классу значений. Если результат функции принадлежности равен 0, то - не относится; если результат равен 1, то - относится; чем ближе результат к 0, тем меньше уверенность принадлежности, а чем ближе результат к 1, тем уверенность больше.
Опишем для каждого признака вектор COND (от англ. conditions - состояния), 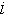 -ый элемент которого есть результат функции принадлежности значения данного признака -ый элемент которого есть результат функции принадлежности значения данного признака 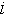 -му классу значений. Для краткости, будем называть класс значения - состоянием. Если -му классу значений. Для краткости, будем называть класс значения - состоянием. Если 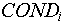 данного признака больше ноля, то будем говорить, что данный признак находится в данного признака больше ноля, то будем говорить, что данный признак находится в 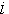 -ом состоянии. -ом состоянии.
В качестве примера приведем возможные результаты функции принадлежности значения простого признака "температура воздуха" объекта "комната" классам значений "холодно", "нормально", "жарко".
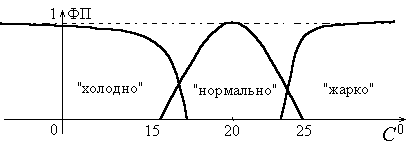
Рисунок 3. Пример возможных результатов функции принадлежности (ФП) значения признака "температура воздуха" объекта "комната".
Совокупность состояний, в которых находятся признаки данного объекта будем называть значением данного объекта. Аналогично значениям признаков, значение объекта можно отнести к классам значений. Например, классы значений объекта "комната" могут быть: "большая светлая комната", "холодная комната", "маленькая комната со старой мебелью" и т. п.
Для каждого класса значений объекта можно определить функцию принадлежности, возвращающую в интервале от 0 до 1 включительно степень уверенности в том, что значение данного объекта относится к данному классу значений. Назовем, для краткости, классы значений объекта - состояниями объекта. Если для принадлежности значений объекта к данному классу значений необходимо, чтобы некоторые признаки данного объекта находились в определенных состояниях, то такие признаки будем называть признаками, описывающими данное состояние объекта.
Опишем для каждого объекта вектор COND (от англ. conditions - состояния), NC-ый элемент которого есть результат функции принадлежности значения данного объекта NC-му состоянию. Аналогично, как и с признаками, будем говорить, что данный объект находится в NC-ом состоянии, если 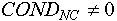 . .
Опишем для каждого объекта матрицу DESC (от англ. descriptions - описания), состоящую из 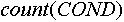 строк и числа колонок, равного числу признаков данного объекта. NC-ая строка DESC хранит сведения о том, какие признаки объекта и в каких своих состояниях являются признаками, описывающими NC-ое состояние объекта. Если строк и числа колонок, равного числу признаков данного объекта. NC-ая строка DESC хранит сведения о том, какие признаки объекта и в каких своих состояниях являются признаками, описывающими NC-ое состояние объекта. Если 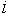 -ый элемент NC-ой строки DESC равен нолю, то признак -ый элемент NC-ой строки DESC равен нолю, то признак 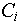 данного объекта не является признаком, описывающим NC-ое состояние данного объекта. Если данного объекта не является признаком, описывающим NC-ое состояние данного объекта. Если 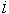 -ый элемент NC-ой строки DESC отличен от ноля, то это - номер состояния, в котором должен находиться -ый элемент NC-ой строки DESC отличен от ноля, то это - номер состояния, в котором должен находиться 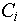 признак в NC-ом состоянии данного объекта. Объект будет находиться в NC-ом состоянии, если все признаки, описывающие данное состояние объекта, находятся в состоянии, указанном соответствующим элементом признак в NC-ом состоянии данного объекта. Объект будет находиться в NC-ом состоянии, если все признаки, описывающие данное состояние объекта, находятся в состоянии, указанном соответствующим элементом 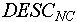 данного объекта. Таким образом, для данного объекта: данного объекта. Таким образом, для данного объекта:
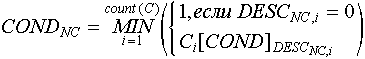
Видно, что результат функции принадлежности значения объекта NC-му состоянию есть минимальное нахождение описывающих NC-ое состояние признаков в необходимых состояниях.
Покажем, в качестве примера, возможный вид матрицы DESC объекта "комната", заменив, для наглядности, номера состояний описывающих признаков названиями этих состояний.
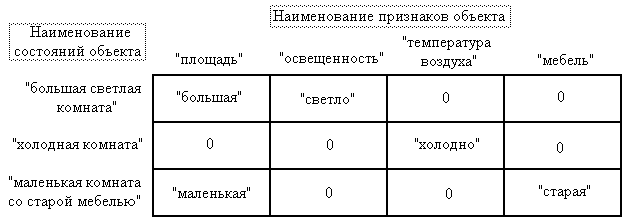
Рисунок 4. Пример матрицы DESC объекта "комната"
Из приведенного рисунка видно, что объект "комната" будет находиться, например, в состоянии "большая светлая комната", если описывающие данное состояние признаки "площадь" и "освещенность" будут находиться в состояниях "большая" и "светло", соответственно.
Некоторые объекты могут быть признаками других объектов, являясь, таким образом, сложными признаками. Как и для любого другого признака, к сведениям о таких вложенных объектах можно обратиться через множество C, содержащееся в сведениях о родительском объекте. Сведения о вложенных объектах хранятся в виде, аналогичном сведениям других объектов - это индексированное множество, состоящее из следующих поименованных элементов:
C - индексированное множество, элементами которого являются сведения о каждом из признаков объекта DESC - матрица, каждая строка которой есть описание одного из состояний объекта (указан состав и состояния каждого из описывающих признаков) COND - вектор, каждый элемент которого есть результат функции принадлежности значения данного объекта к состоянию, описанном соответствующей строкой DESC
В качестве примера приведем возможный состав сведений о объекте "здание" одним из признаков которого является ранее упоминавшийся объект "комната".
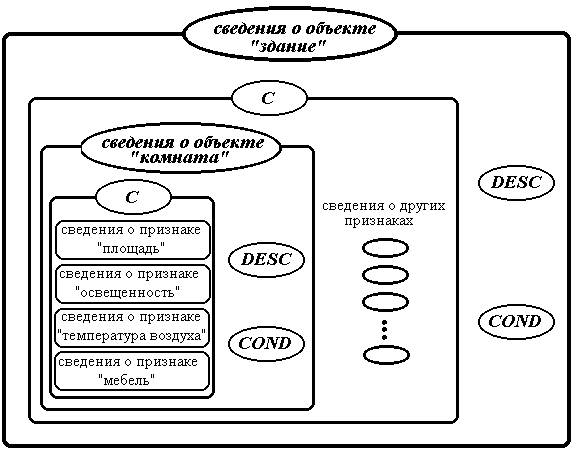
Рисунок 5. Пример состава сведений о объекте "здание", сложным признаком которого является объект "комната"
Понятие контейнера
В ряде задач необходим представить группу однотипных объектов в качестве одного объекта, когда большую роль играют сведения не столько о свойствах каждого конкретного объекта группы, сколько сведения о свойствах всей группы, как одного целого. Будем называть такую группу контейнерным объектом, или просто - контейнером, а объекты, входящие в группу - объектами контейнера.
Объекты контейнера - это признаки контейнерного объекта. Состав сведений о контейнерном объекте аналогичен составу сведений о любом другом объекте - это индексированной множество, элементы которого - C, DESC и COND; однако способ описания состояний контейнера и способ вычисления функции принадлежности к состоянию отличен от других объектов. Укажем также, что в отличии от объектов-не-контейнеров, строки DESC в описании объекта-контейнера могут содержать отличное друг от друга количество элементов.
По степени взаимосвязи объектов контейнера можно выделить следующие виды контейнеров:
- непозиционный контейнер
- позиционный контейнер (открытый и замкнутый)
- полупозиционный контейнер (открытый и замкнутый)
Каждый из видов контейнера использует собственный способ описания состояний и вычисления функции принадлежности состояниям. Рассмотрим каждый из видов контейнеров подробнее.
Непозиционный контейнер
Объекты непозиционного контейнера не связаны между собой, в рамках конкретной предметной области, отношениями, позволяющими выделять для какого-либо из объектов объект, предшествующий данному, и объект, следующий за данным. Непозиционный контейнер - это выступающая как одно целое группа однотипных объектов, не связанных между собой отношениями "следовать" и "предшествовать".
Классификация значения непозиционного контейнера проводится по наличию среди объектов контейнера непересекающихся, определенного размера групп объектов, находящихся в определенном для каждой группы состоянии.
Способ описания NC-го состояния непозиционного контейнера состоит в следующем:
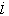 -ый элемент NC-ой строки DESC контейнера показывает, что в группу объектов контейнера, находящихся в состоянии, указанном -ый элемент NC-ой строки DESC контейнера показывает, что в группу объектов контейнера, находящихся в состоянии, указанном 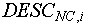 , должно входить на один объект больше, чем при рассмотрении первых , должно входить на один объект больше, чем при рассмотрении первых 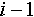 элементов NC-ой строки DESC. элементов NC-ой строки DESC.
Пример: пусть NC-ая строка DESC некоторого непозиционного контейнера выглядит следующим образом:
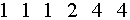
то, следовательно, данный контейнер будет находиться в NC-ом состоянии, если среди объектов, его составляющих, можно найти следующие непересекающиеся группы:
группа из трех объектов, находящихся в первом состоянии (т. е.  которых отличен от ноля) которых отличен от ноля) группа из одного объекта, находящегося во втором состоянии группа из двух объектов, находящихся в четвертом состоянии объекты, не вошедшие ни в одну из выше перечисленных групп, образуют группу объектов, состояние которых безразлично для NC-го состояния контейнера.
Рассмотрим функцию НПГ (НеПозиционного контейнера Группы), представляющую собой функцию принадлежности значения данного непозиционного контейнера NC-му состоянию:
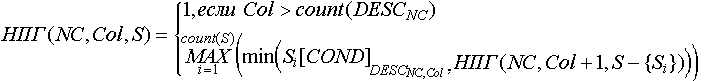
Здесь: NC - номер данного состояния контейнера; Col - номер данного элемента описания NC-го состояния; S - индексированной множество объектов, еще не вошедших ни в одну из групп.
Первая альтернатива заканчивается успехом , так как были просмотрены все элементы описания.
Вторая альтернатива среди еще не использованных объектов контейнера ищет такой, который максимально находился бы в состоянии, указанным данным элементом описания, и исключение которого из S позволило бы, тем не менее, получить максимальный результат НПГ для следующего элемента описания.
Соответственно, для данного непозиционного контейнера:
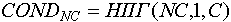
В качестве примера непозиционного контейнера приведем сложный признак "мебель" объекта "комната", ранее уже упоминавшегося. Здесь, "мебель" - это группа однотипных объектов "предмет мебели", выступающая как единое целое. В рамках нашего примера будем считать, что объекты данного контейнера не связаны между собой отношениями "следовать" и "предшествовать", тогда "мебель" - это непозиционный контейнерный объект, выступающий в роли сложного признака объекта "комната". Будем считать, что "мебель" в "комнате" находится в состоянии "старая", если будет найдено как минимум два "предмета мебели", находящихся в состоянии "старый предмет мебели". Покажем описание состояния "старая" непозиционного контейнера "мебель".

Рисунок 6. Cтрока DESC, описывающая состояние "старая" непозиционного контейнера "мебель"
На рисунке мы, для наглядности, вместо номера состояния "старый предмет мебели" указали просто название этого состояния. Видно, что непозиционный контейнер "мебель" будет находится в состоянии "старая", если среди объектов контейнера - "предметов мебели", будет найдено два объекта, находящихся в состоянии "старый предмет мебели".
Позиционный контейнер
Позиционный контейнер - это выступающая как одно целое группа однотипных объектов, связанных между собой отношением "следовать" следующим образом:
- Каждый объект контейнера может быть связан отношением "следовать" не более чем с одним объектом (т. е. каждому объекту контейнера можно сопоставить не более одного другого объекта, называемого "следующим" по отношению к данному)
- Среди объектов контейнера может существовать не более одного объекта, не имеющего объекта-предшественника, и не более одного объекта, не имеющего следующего объекта.
- Среди объектов контейнера должен существовать по крайней мере один объект, начиная с которого и переходя к каждому следующему, можно перебрать таким образом все объекты контейнера. Будем такой объект называть началом цепочки.

Рисунок 7. Объект А связан с объектом В отношением "следовать". Объект А является для В объектом-предшественником, а объект В является для А следующим объектом.
По числу объектов, способных выступить в роли начала цепочки, можно выделить два вида позиционных контейнеров:
- Позиционный открытый контейнер - существует единственный объект, способный выступить в роли начала цепочки. Этот объект не имеет объекта-предшественника. Среди объектов позиционного открытого контейнера можно выделить также единственный конец цепочки - объект, который не имеет следующего объекта.
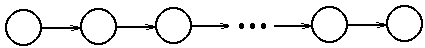
Рисунок 8. Объекты позиционного открытого контейнера
- Позиционный замкнутый контейнер - любой объект контейнера может выступить в роли начала цепочки. Каждый из объектов имеет и объект-предшественник и следующий объект.
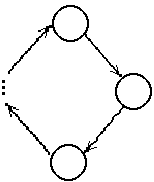
Рисунок 9. Объекты позиционного замкнутого контейнера
Классификация значения позиционного контейнера проводится по наличию среди его объектов, начиная поиск с начала цепочки, следующих в определенном порядке некоторых непересекающихся последовательностей объектов, находящихся в определенных состояниях. Последовательности объектов, находящихся в определенных состояниях могут быть отделены друг от друг некоторыми, не имеющими значение для данного класса значения контейнера, последовательностями объектов, находящихся в любых состояниях.
В качестве примера позиционного контейнера можно привести некоторое предложение на естественном языке. Предложение - это позиционный контейнер, так как это выступающая как одно целое группа символов (букв, цифр, пробелов, знаков препинания) связанных между собой отношением "следовать". Предложение - открытый контейнер, так как существует только один объект (первая буква предложения), начиная с которого и переходя к каждому следующему, можно перебрать таким образом все объекты контейнера. При классификации значения предложения, как позиционного контейнера, обращается внимание на наличие в нем идущих в определенном порядке некоторых последовательностей символов - слов.
Способ описания состояния позиционного контейнера следующий:
- Если необходимо, что бы в данном состоянии контейнера некоторый объект находился в определенном состоянии, то будем описании использовать некоторый элемент, равный номеру необходимого состояния объекта контейнера
- Последовательность отличных от ноля и расположенных подряд элементов описания, состоящая из N членов, показывает, что среди объектов контейнера должна находиться последовательность из N объектов, каждый из которых находится в состоянии, указанным соответствующим членом данной последовательности элементов описания. Первый объект последовательности объектов должен находиться в состоянии, указанном первым элементов последовательности элементов описания; второй объект - в состоянии, указанном вторым элементом; третий объект - третьим элементом и т. д.
- Возможность наличия произвольной последовательности находящихся в любых состояниях объектов будем указывать в описании элементом равным нолю.
Таким образом, описание состояния позиционного контейнера будет представлять собой описание некоторых последовательностей объектов контейнера.
Позиционный контейнер будет находиться в данном состоянии, если:
- Среди объектов контейнера, начиная поиск с начала цепочки и переходя к каждому следующему объекту, будут найдены все последовательности, указанные в описании данного состояния
- Последовательности будут обнаружены в том же порядке, в каком они даны в описании
- Обнаруженные последовательности не будут пересекаться - т. е. не будут содержать общих объектов
- Каждый объект контейнера удастся включить в какую-либо последовательность
Пусть, например предложение, как позиционный контейнер, будет находиться в состоянии "заказ на ремонт автомобиля", если где-то в данном предложении находится слово "отремонтируйте", после которого, возможно не сразу, находится слово "машину", тогда описание данного состояния предложенным способом будет как:
0 "отремонтируйте" 0 "машину" 0
Здесь, в кавычках, вместо последовательности номеров состояний объектов предложения, для наглядности указаны буквы, как названия состояний объектов контейнера.
В описанном состоянии будут находиться, например, следующие предложения:
"Отремонтируйте машину. "
"Пожалуйста, отремонтируйте мою машину. "
"Пожалуйста, отремонтируйте мою машину к следующей пятнице. "
Будем считать, что сведения о объектах позиционного контейнера находятся в его индексированном множестве С таким образом, что перебирая эти сведения по их индексам, от 1 до count(C), мы все время будем переходить от сведений о объекте-предшественнике к сведениям о следующем ему объекте.
Рассмотрим функцию ПГ (Позиционного контейнера Группы), представляющую собой функцию принадлежности значения позиционного контейнера NC-му состоянию.
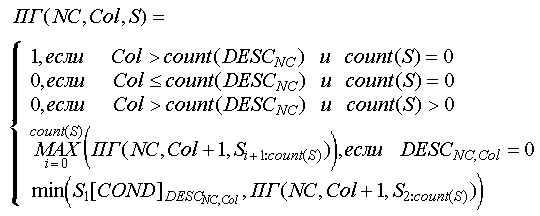
Здесь: NC - номер данного состояния; Col - номер данного элемента описания NC-го состояния; S - индексированное множество объектов контейнера, еще не вошедших ни в одну из последовательностей
Первая альтернатива заканчивается успехом, так как были просмотрены все элементы описания и не осталось ни одного не использованного объекта.
Вторая альтернатива заканчивается неуспехом, так как были просмотрены еще не все элементы описания, а не использованных объектов не осталось.
Третья альтернатива заканчивается неуспехом, так как были просмотрены все элементы описания, но остались объекты, не вошедшие не в одну из последовательностей.
Четвертая альтернатива - поскольку данный элемент описания равен нолю, то в произвольную последовательность из S берется такое количество первых объектов, которое позволило бы оставшиеся объекты наиболее оптимально разбить на последовательности, описанные в оставшейся части описания.
Пятая альтернатива - первый неиспользованный объект должен находиться в состоянии, указанном данным элементом описания, а остальные объекты должны быть наиболее оптимально разбиты на последовательности, описанные в оставшейся части описания.
Функция ПГ возвращает наименьшее нахождение одного из объектов контейнера в необходимом состоянии, и входящего в одну из не произвольных (т. е. не описанных как 0) последовательностей.
Таким образом, для открытого позиционного контейнера:
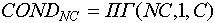
В случае, если данный позиционный контейнер является замкнутым (т. е. любой из объектов контейнера может выступить в роли начала цепочки), то будем просматривать count(C) вариантов вызова ПГ, в каждом из которых очередной объект контейнера выступает в роли начала цепочки. Максимальный результат ПГ возьмем в качестве результата функции принадлежности к NC-му состоянию:

Полупозиционный контейнер
Полупозиционный контейнер - это выступающая как единое целое группа однотипных объектов, связанных между собой отношением "следовать" следующим образом:
- Каждый объект контейнера может быть связан отношением "следовать" не более чем с одним объектом (т. е. каждому объекту контейнера можно сопоставить не более одного другого объекта, называемого "следующим" по отношению к данному)
- Среди объектов контейнера может существовать не более одного объекта, не имеющего объекта-предшественника, и не более одного объекта, не имеющего следующего объекта.
- Среди объектов контейнера должен существовать по крайней мере один объект, начиная с которого и переходя к каждому следующему, можно перебрать таким образом все объекты контейнера. Будем такой объект называть началом цепочки.
По числу объектов, способных выступить в роли начала цепочки, можно выделить два вида полупозиционных контейнеров:
- Полупозиционный открытый контейнер - существует единственный объект, способный выступить в роли начала цепочки. Этот объект не имеет объекта-предшественника. Среди объектов полупозиционного открытого контейнера можно выделить также единственный конец цепочки - объект, который не имеет следующего объекта.
- Полупозиционный замкнутый контейнер - любой объект контейнера может выступить в роли начала цепочки. Каждый из объектов имеет и объект-предшественник и следующий объект.
В отличие от позиционного контейнера, классификация значения полупозиционного контейнера проводится по наличию в его составе, следующих в ЛЮБОМ порядке некоторых непересекающихся последовательностей объектов, находящихся в определенных состояниях. Таким образом, полупозиционный контейнер будет находиться в данном состоянии, если:
- Среди объектов контейнера, начиная поиск с начала цепочки и переходя к каждому следующему объекту, будут найдены все последовательности, указанные в описании
- Найденные последовательности не будут пересекаться (т. е. содержать общих объектов)
Способ описания состояния полупозиционного контейнера следующий:
- Если необходимо, что бы в данном состоянии контейнера некоторый объект находился в определенном состоянии, то будем в описании использовать некоторый элемент, равный номеру необходимого состояния объекта контейнера
- Последовательность больших ноля и расположенных подряд элементов описания, состоящая из N членов, показывает, что среди объектов контейнера должна находиться последовательность из N объектов, каждый из которых находится в состоянии, указанным соответствующим членом данной последовательности элементов описания. Первый объект последовательности объектов должен находиться в состоянии, указанном первым элементов последовательности элементов описания; второй объект - в состоянии, указанном вторым элементом; третий объект - третьим элементом и т. д.
- Возможность наличия произвольной последовательности, находящихся в любых состояниях объектов, и расположенной между двумя последовательностями, описанными элементами описания большими ноля, будем указывать в описании элементом равным нолю и расположенным между соответствующими последовательностями элементов больших ноля.
- Для разделения описаний последовательностей, которые могут следовать в любом порядке, будем использовать элемент описания меньший ноля.
Будем считать, что сведения о объектах полупозиционного контейнера находятся в его индексированном множестве С таким образом, что перебирая эти сведения по их индексам, от 1 до count(C), мы все время будем переходить от сведений о объекте-предшественнике к сведениям о следующем ему объекте.
Рассмотрим функцию ППГ (ПолуПозиционного контейнера Группы), представляющую собой функцию принадлежности значения полупозиционного контейнера NC-му состоянию.
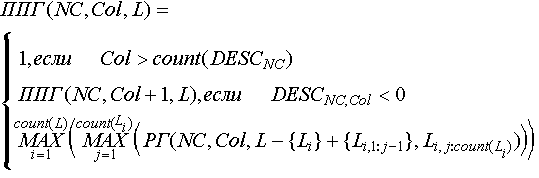
Здесь: NC - номер данного состояния; Col - номер элемента NC-го состояния; L - индексированное множество, элементами которого являются найденные и неиспользованные последовательности объектов.
Первая альтернатива заканчивается успехом, поскольку все элементы описания были просмотрены.
Вторая альтернатива - поскольку был найден отрицательный элемент, сигнализирующий о окончании описания данной последовательности объектов, то ищется описание следующей последовательности.
Третья альтернатива - в каждом элементе L (найденные и еще неиспользованные последовательности объектов), ищется возможность, начиная с j-го объекта последовательности, построить последовательность объектов, начало которой описано данным элементом описания; первые j-1 объектов i-ой неиспользованной последовательности возвращаются в L.
Функция РГ (Размещение Группы):
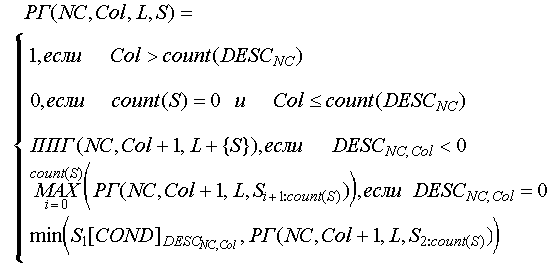
Здесь: NC - номер данного состояния; Col - номер данного элемента описания NC - го состояния; L - индексированное множество, элементами которого являются найденные и неиспользованные последовательности объектов; S - данная, не входящая в L, последовательность объектов, в которой пытаются найти часть, являющаяся последовательностью, указанной в описании.
Первая альтернатива заканчивается успехом, поскольку все элементы описания данного состояния были просмотрены.
Вторая альтернатива заканчивается неуспехом, поскольку не все элементы описания были просмотрены, а неиспользованных объектов в S уже не осталось.
Третья альтернатива - был обнаружен меньший ноля элемент описания. Это показывает, что описание данной последовательности окончено, поэтому в L возвращается оставшаяся неиспользованной часть S и происходит дальнейший просмотр описания.
Четвертая альтернатива - был обнаружен равный нолю элемент описания. Это показывает наличие произвольной длины последовательности объектов, находящихся в любых состояниях. Ищется оптимальный состав такой последовательности из первых объектов S, при котором размещение последовательностей, указанных в оставшейся части описания было бы оптимальным (т. е. стремящимся к 1).
Пятая альтернатива - первый неиспользованный объект S должен находиться в состоянии, указанном данным элементом описания, а остальные объекты должны наиболее оптимально разбиты на последовательности, указанные в оставшейся части описания.
Соответственно для открытого полупозиционного контейнера получаем:
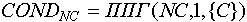
В случае, если данный полупозиционный контейнер является замкнутым (т. е. любой из объектов контейнера может выступить в роли начала цепочки), то будем просматривать count(C) вариантов вызова ППГ, в каждом из которых очередной объект контейнера выступает в роли начала цепочки. Максимальный результат ППГ возьмем в качестве результата функции принадлежности к NC-му состоянию:

В обоих случаях в качестве единственной (до начала расчета) и еще не использованной последовательности объектов передаются все объекты контейнера в порядке их следования, от начала цепочки и к каждому следующему.
Рассмотрим функцию COMP, возвращающую в интервале от 0 до 1 включительно степень подобия двух однотипных (т. е. обладающих одинаковым количественным и семантическим набором признаков) объектов.
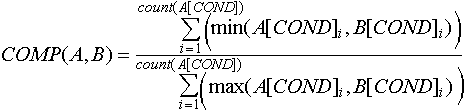
Результат функции есть отношение объема пространства состояний, в которых находятся оба объекта, к объему пространства состояний, в которых находится хотя бы один из объектов.
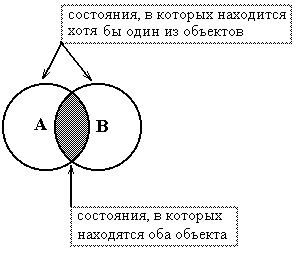
Рисунок 10. Пространства, состояний, в которых находятся объекты А и В.
На рисунке, степень подобия двух объектов есть отношение площади заштрихованного участка к площади всей фигуры.
В тех случаях, когда объекты контейнеров образуют последовательности (имеется в виду объекты позиционного и полупозиционного контейнера), возможным классификационным правилом может быть наличие одинаковых последовательностей объектов. Предложенные ранее способы описания состояния позиционного, или полупозиционного, контейнера не позволяли обнаруживать равенство некоторых последовательностей объектов. Рассмотрим другой, видоизмененный способ описания, избавленный от подобного недостатка.
Будем меньшим ноля элементом описания обозначать некоторую последовательность объектов, находящихся в любых состояниях. Одним и тем же отрицательным числом мы будем отмечать одинаковые последовательности объектов. Элементом, большим ноля, мы будем показывать, что должен существовать объект, находящийся в состоянии, указанном данным элементом. Элементом, равным нолю, мы будем в описании состояния полупозиционного контейнера отделять друг от друга описания последовательностей, которые могут следовать в произвольном порядке. В описании состояния позиционного контейнера элементы, равные нолю, использовать не будем, так как произвольную последовательность, как уже говорилось, будем отмечать отрицательным элементом.
Будем называть отметку (значение отрицательного элемента описания), о наличии произвольной последовательности объектов - переменной описания. Отрицательный элемент, обозначающий данную переменную описания будем использовать в качестве имени переменной. Обнаруженную последовательность объектов, соответствующую данной переменной описания, будем называть - значением данной переменной. Каждому упоминанию переменной (т. е. каждому элементу, равному имени данной переменной) будет соответствовать некоторая последовательность объектов контейнера, следовательно одна переменная может иметь несколько значений одновременно.. Судить о степени нахождения контейнера в определенном состоянии мы будем, помимо прочего, и по тому, насколько равны между собой значения каждой из переменных, упоминающихся в описании данного состояния.
В случае позиционного контейнера, данный контейнер будет находиться в определенном состоянии, если:
- Каждому, меньшему ноля, элементу описания будет найдена соответствующая последовательность объектов, находящихся в любых состояниях.
- Каждому, большему ноля, элементу описания будет найдена последовательность, состоящая из одного объекта, находящегося в состоянии, указанном данным элементом описания.
- Все найденные последовательности не должны пересекаться и должны следовать в том же порядке, в коком они указаны в описании состояния, начиная просмотр с первого элемента и по порядку их индексов к последнему.
- Каждый объект контейнера должен входить в какую либо последовательность, соответствующую какому-либо элементу описания данного состояния
- Последовательности объектов, соответствующие одинаковым отрицательным элементам описания, должны быть равны друг другу; т. е. значения каждой из переменных описания должны быть равны.
Рассмотрим, например, следующее описание некоторого арифметического выражения, как открытого позиционного контейнера, объектами которого являются буквы, цифры, математический символы и т. д. :
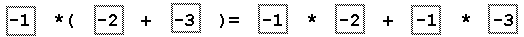
Здесь, для наглядности, элементы, обозначающие переменные, были заключены в рамки, а элементы, обозначающие определенные состояния, представлены символами, соответствующими этим состояниям. Тогда, объект "a*(b+c)=a*b+a*c" будет находиться в описанном состоянии, также, как и объект "sin(x)*(cos(y)+tg(z))=sin(x)*cos(y)+sin(x)*tg(z)". Однако, объект "a*(b+c)=a*R+a*c" не может находиться в описанном состоянии, поскольку здесь для переменной, поименованной в описании как -2, нельзя найти одинаковые значения ("b" не равен "R").
Для работы с переменными описания будем использовать в функциях принадлежности индексированное множество VAL. Каждый из элементов VAL поименован отрицательным числом и представляет собой - индексированное множество, элементы которого - значения соответствующей переменной. Значение переменной - индексированное множество, элементы которого - объекты, расположенные таким образом, что перебирая их по порядку следования их индексов, мы будем постоянно переходить от объекта предшественника к следующему ему объекту.
Рассмотрим функцию EqvSeq, возвращающую в интервале от 0 до 1 включительно степень подобия двух последовательностей (значений переменной):
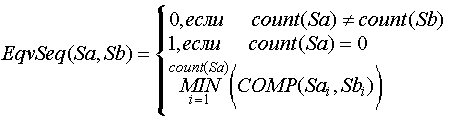
Здесь: Sa, Sb - сравниваемые последовательности объектов.
Таким образом, равными последовательностями будем считать последовательности, состоящие из одинакового числа объектов таких, что объекты с одинаковыми индексами равны.
Рассмотрим функцию EQV возвращающую в интервале от 0 до 1 включительно степень подобия значений переменной:
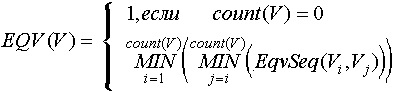
Здесь: V - индексированное множество, элементы которого - значения одной переменной.
Таким образом, функция принадлежности значения открытого позиционного контейнера, дающая возможность работы с переменными:
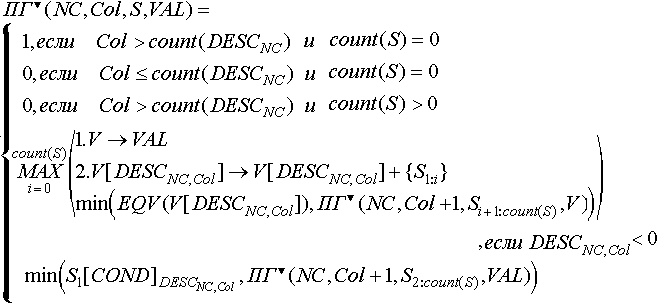
Здесь: NC - номер данного состояния; Col - номер данного элемента описания NC-го состояния; S - последовательность еще не использованных объектов контейнера; VAL - индексированное множество, каждый элемент которого, поименованный некоторым отрицательным числом, - индексированное множество значений соответствующей переменной описания.
Первая альтернатива заканчивается успехом, так как были просмотрены все элементы описания и не осталось не использованных объектов.
Вторая альтернатива заканчивается неуспехом, так как были просмотрены не все элементы описания, но не осталось неиспользованных объектов.
Третья альтернатива заканчивается неуспехом, так как были просмотрены все элементы описания, но еще не все объекты были использованы.
Четвертая альтернатива - был обнаружен элемент описания, указывающий на переменную. Происходит следующее:
Создается V - копия VAL (п. 1). а) если в V нет элемента (индексированного множества значений соответствующей переменной), поименованного значением 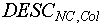 , то он создается и его первым элементом становится последовательность , то он создается и его первым элементом становится последовательность 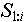 (п. 2). (п. 2).
б) если в V существует элемент, поименованный значением 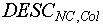 , то в этот элемент (индексированной множество значений соответствующей переменной) добавляется новое значение переменной - последовательность , то в этот элемент (индексированной множество значений соответствующей переменной) добавляется новое значение переменной - последовательность 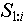 (п.2). (п.2).
В обоих случаях 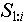 - это последовательность объектов, которую мы пытаемся взять в качестве одного из значений переменной. - это последовательность объектов, которую мы пытаемся взять в качестве одного из значений переменной.
Правильность найденной последовательности проверяется степенью подобия значений переменной, на которую ссылается данный элемент описания; и успехом поиска последовательностей, описанных в оставшейся части описания
Пятая альтернатива - 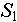 должен находиться в состоянии, указанном данным элементом описания; и поиск последовательностей, описанных в оставшейся части описания должен закончиться успехом. должен находиться в состоянии, указанном данным элементом описания; и поиск последовательностей, описанных в оставшейся части описания должен закончиться успехом.
Соответственно, для позиционного открытого контейнера:
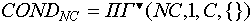
В случае позиционного замкнутого контейнера:
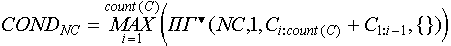
В обоих случаях в качестве единственной еще неиспользованной последовательности объектов передаются все объекты контейнера в порядке их следования от начала цепочки и к каждому следующему; в качестве VAL передается пустое множество, так как до начала просмотра еще ни одна переменная не обнаружена.
Полупозиционный контейнер будет находиться в некотором состоянии, если:
- Каждому, меньшему ноля, элементу описания будет найдена соответствующая последовательность объектов, находящихся в любых состояниях.
- Каждому, большему ноля, элементу описания будет найдена последовательность, состоящая из одного объекта, находящегося в состоянии, указанном данным элементом описания.
- Все найденные последовательности не должны пересекаться
- Последовательности, описания которых не разделены равным нолю элементом, должны следовать в том же порядке, в каком они указаны в описании состояния, начиная просмотр с первого элемента и по порядку их индексов к последнему.
- Последовательности, описания которых разделены равным нолю элементом, могут следовать в произвольном порядке относительно друг друга.
- Последовательности объектов, соответствующие одинаковым отрицательным элементам описания, должны быть равны друг другу; т. е. значения каждой из переменных описания должны быть равны.
Рассмотрим функцию, представляющую собой функцию принадлежности значения полупозиционного открытого контейнера NC-му состоянию, и дающую возможность работы с переменными описания:
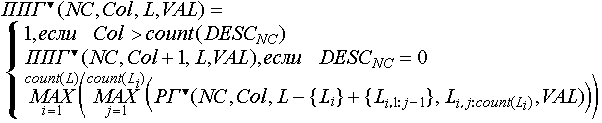
Здесь: NC - номер данного состояния; Col - номер данного элемента описания NC-го состояния; L - индексированное множество обнаруженных, но еще не использованных последовательностей объектов; VAL - индексированное множество, каждый элемент которого, поименованный некоторым отрицательным числом, - индексированное множество значений соответствующей переменной описания.
Первая альтернатива заканчивается успехом, так как были просмотрены все элементы описания.
Вторая альтернатива - был найден элемент, разделяющий описания последовательностей, которые могут следовать в любом порядке; здесь ищем описание следующей последовательности.
Третья альтернатива - поиск последовательности объектов, наиболее оптимального соответствующей обнаруженному описанию последовательности.
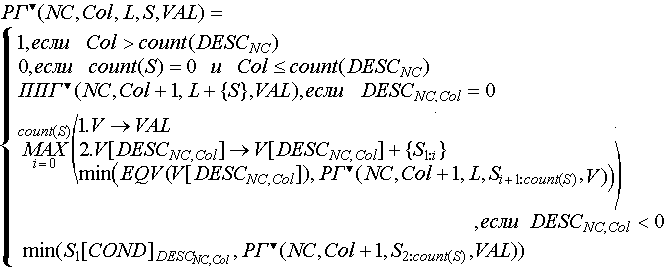
Здесь: NC - номер данного состояния; Col - номер данного элемента описания NC-го состояния; L - индексированное множество обнаруженных, но еще не использованных последовательностей объектов; S - источник формирования последовательности объектов, указанной в описании; VAL - индексированное множество, каждый элемент которого, поименованный некоторым отрицательным числом, - индексированное множество значений соответствующей переменной описания.
Первая альтернатива заканчивается успехом, так как были просмотрены все элементы описания.
Вторая альтернатива заканчивается неуспехом, так как все объекты S были использованы, но еще не все элементы описания были просмотрены.
Третья альтернатива - был найден равный нолю элемент описания, показывающий, что необходимо искать описание следующей последовательности. Здесь происходит возврат неиспользованной части S в L, в качестве еще одной обнаруженной но еще не использованной последовательности объектов.
Четвертая альтернатива - - был обнаружен элемент описания, указывающий на переменную. Происходит следующее:
Создается V - копия VAL (п. 1). а) если в V нет элемента (индексированного множества значений соответствующей переменной), поименованного значением 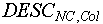 , то он создается и его первым элементом становится последовательность , то он создается и его первым элементом становится последовательность 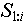 (п. 2). (п. 2).
б) если в V существует элемент, поименованный значением 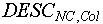 , то в этот элемент (индексированной множество значений соответствующей переменной) добавляется новое значение переменной - последовательность , то в этот элемент (индексированной множество значений соответствующей переменной) добавляется новое значение переменной - последовательность 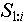 (п.2). (п.2).
В обоих случаях 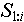 - это последовательность объектов, которую мы пытаемся взять в качестве одного из значений переменной. - это последовательность объектов, которую мы пытаемся взять в качестве одного из значений переменной.
Правильность найденной последовательности проверяется степенью подобия значений переменной, на которую ссылается данный элемент описания; и успехом поиска последовательностей, описанных в оставшейся части описания
Пятая альтернатива - 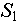 должен находиться в состоянии, указанном данным элементом описания; и поиск последовательностей, описанных в оставшейся части описания должен закончиться успехом. должен находиться в состоянии, указанном данным элементом описания; и поиск последовательностей, описанных в оставшейся части описания должен закончиться успехом.
Таким образом, для открытого полупозиционного контейнера:
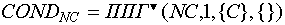
В случае замкнутого полупозиционного контейнера:
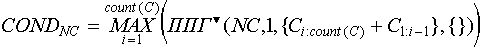
В обоих случаях в качестве единственной еще неиспользованной последовательности объектов передаются все объекты контейнера в порядке их следования от начала цепочки и к каждому следующему; в качестве VAL передается пустое множество, так как до начала просмотра еще ни одна переменная не обнаружена.
Отнесение некоторого объекта к какому либо из классов, представленных в обучающей выборке, будем производить на базе сравнения сведений о данном объекте со сведениями о объектах обучающей выборки, относящихся к данному классу.
Степень уверенности отнесения объекта CurObj, представленного в виде его описания, к классу с индексом CL в CLASSES, будем считать равной среднему подобию CurObj объектам обучающей выборки, относящимся к данному классу:
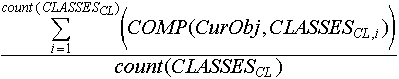
Соответственно, выражение:

возвращает номер класса (его индекс в CLASSES), к которому с наибольшей степенью уверенности можно отнести объект CurObj.
Основной проблемой при программной реализации системы распознавания образов является нахождение возможных состояний объектов. В случае, если перечень возможных состояний изначально задан, то реализовать их перебор для сравнения объектов достаточно просто, однако в случае, если классификационные правила априорно не известны, то число возможных состояний объекта может быть достаточно большим - даже в простых случаях может измеряться десятками и сотнями миллионов. Таким образом, следует рассмотреть две основные проблемы программной реализации:
- Генерация перечня описаний возможных состояний - поскольку перечень описаний возможных состояний не задается заранее, то он должен быть сгенерирован программно.
- Одновременное наличие в машинной памяти описаний большого числа состояний представляется проблематичным, так как объем машинной памяти ограничен и может быть быстро исчерпан.
Рассмотрим решение указанных проблем.
1. В случае, если объект - не контейнер. Здесь описание состояния будет состоять из 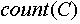 элементов, где С - индексированное множество признаков данного объекта. элементов, где С - индексированное множество признаков данного объекта.
Представим, что описание - это некоторое число, записанное в 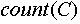 разрядах, причем каждый разрядах, причем каждый 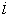 -ый разряд записан в -ый разряд записан в 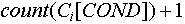 -ричной системе счисления, при -ричной системе счисления, при 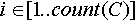 . Тогда число возможных состояний объекта равно: . Тогда число возможных состояний объекта равно:
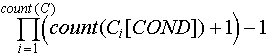
Матрица DESC, описывающая все возможные состояния объекта:
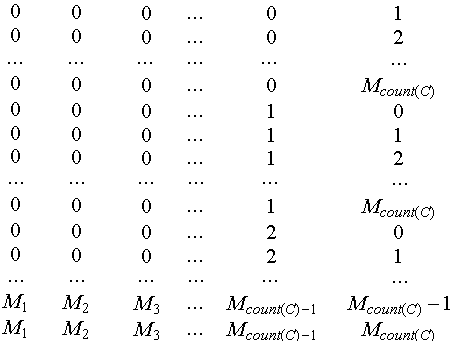
Здесь 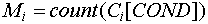 при при 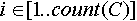 - т. е. число возможных состояний - т. е. число возможных состояний 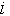 -го признака. -го признака.
2. В случае контейнерного объекта. Описание состояния контейнера также можно представить как число, записанное несколькими разрядами, однако, в отличии от объекта-не-контейнера, каждый из разрядов записан в 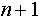 -ричной системе счисления, где -ричной системе счисления, где 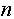 - число возможных состояний объектов контейнера, т. е. системы счисления разрядов равны. - число возможных состояний объектов контейнера, т. е. системы счисления разрядов равны.
2. 1. Контейнер непозиционный. Алгоритм генерации описания всех возможных состояний:

Здесь 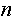 - число возможных состояний объектов контейнера. - число возможных состояний объектов контейнера.
2. 2. Контейнер не-непозиционный. Пусть описание состояния может включать в себя максимум 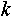 элементов, тогда описание также можно представить как некоторое число, записанное в элементов, тогда описание также можно представить как некоторое число, записанное в 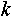 разрядах. Каждый разряд записан в: разрядах. Каждый разряд записан в:
а) Если переменные описания не используются:
а. 1. ) Контейнер позиционный: 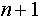 -ричной системе счисления -ричной системе счисления
а. 2. ) Контейнер полупозиционный: 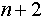 -ричной системе счисления -ричной системе счисления
б) Если переменные описания используются:
б. 1. ) Контейнер позиционный: 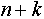 -ричной системе счисления -ричной системе счисления
б. 2. ) Контейнер полупозиционный: 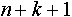 -ричной системе счисления -ричной системе счисления
Здесь 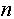 - число возможных состояний объектов контейнера. - число возможных состояний объектов контейнера.
Таким образом получить перечень всех возможных состояний объекта можно перебирая все возможные числа, записанные в 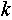 разрядах, разрядах, 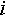 -ый разряд записан в -ый разряд записан в 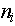 -ричной системе счисления при -ричной системе счисления при 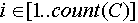 . Здесь . Здесь 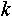 и и 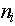 зависят от типа объекта. зависят от типа объекта.
К сожаления предложенный способ генерации перечня описания возможных состояний в случае контейнеров (кроме непозиционных) не позволяет отсеять неуникальные состояния - некоторые обнаруженные состояния будут эквивалентными.
Итак, мы нашли способ, позволяющий нам получить описания всех возможных состояний объекта. Однако, не имеет смысла при распознании рассматривать все возможные состояния и хранить их одновременно в машинной памяти, так как нас интересуют только состояния в которых объект находится, причем не столько сами эти состояния, сколько объем пространства состояний, в которых находится объект - т. е. сумма степеней уверенности в том, что объект находится в этих состояниях.
Рассмотрим способ генерации описаний возможных состояний объекта, позволяющий переходить от одного описания состояния в котором находится объект, к описанию другого состояния, в котором с высокой вероятностью также находится данный объект. Это позволит просматривать не весь перечень возможных состояний, а лишь часть его, включающую все состояния в которых объект находится.
Поскольку при переборе описаний всех возможных состояний мы при переходе от одного описания к следующему изменяем лишь некоторые разряды числа-описания, то, например, в случае объекта-не-контейнера достаточно проверить, находятся ли соответствующие признаки в состояниях указанных измененными разрядами, если нет - то объект не находится в состоянии, указанном вновь сгенерированным описанием и, следовательно, необходима генерация описания следующего состояния (пока это возможно - изменением уже модифицированных разрядов). В общем случае - для каждого из разрядов генерируется перечень его возможных значений и описания состояний, в которых разряд имеет значение, отсутствующее в перечне, - не рассматриваются. Такой способ позволяет значительно сократить число просматриваемых описаний состояний, в которых объект не находится, а в случае объекта-не-контейнера и вовсе исключить описания таких состояний из рассмотрения.
При программной реализации будем использовать следующий алгоритм вычисления степени подобия двух объектов 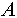 и и 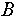 : :
- Пусть
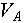 - объем пространства состояний, в которых находится объект - объем пространства состояний, в которых находится объект 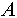
- Пусть
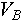 - объем пространства состояний, в которых находится объект - объем пространства состояний, в которых находится объект 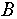 . .
- Пусть
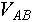 - объем пространства состояний, в которых находятся оба объекта - объем пространства состояний, в которых находятся оба объекта
- Степень подобия объектов
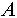 и и 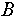 равна: равна:
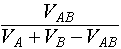
Поясним значение знаменателя следующим рисунком:
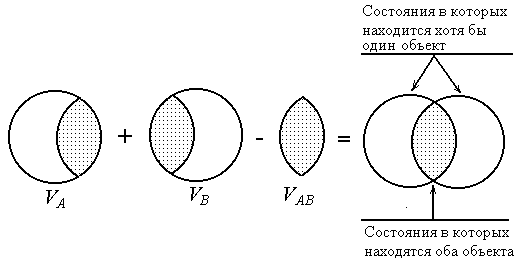
Рисунок 11. Сравнение объектов
На рисунке, степень подобия есть отношение площади заштрихованного участка к площади всей фигуры (двух пересекающихся окружностей).
Найти 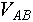 можно при вычислении либо можно при вычислении либо 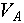 либо либо 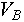 , так как если было найдено некоторое состояние, в котором находится, например, объект , так как если было найдено некоторое состояние, в котором находится, например, объект 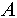 , то имеет смысл сразу проверить степень нахождения в этом состоянии и объекта , то имеет смысл сразу проверить степень нахождения в этом состоянии и объекта 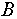 , а минимум из двух этих величин есть степень нахождения обоих этих объектов в данном состоянии. Это сэкономит время вычислений поскольку не будет необходимости отдельно вычислять , а минимум из двух этих величин есть степень нахождения обоих этих объектов в данном состоянии. Это сэкономит время вычислений поскольку не будет необходимости отдельно вычислять 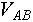 заново перебирая перечень возможных состояний. заново перебирая перечень возможных состояний.
Таким образом функционирование системы распознавания образов представим как:
I. Обучение
1. Получение обучающей выборки
2. Подсчет для каждого из объектов обучающей выборки объема пространства состояний, в которых находится данный объект.
II. Эксплуатация
1. Получение некоторого объекта (его описания) на вход системы распознавания образов (ОПХ - объект, поступивший на вход)
2. Распознавание
2. 1. Вычисление объема пространства состояний, в которых находится ОПХ
2. 2. Для каждого из объектов обучающей выборки находится объем пространства состояний в которых находится данный объект обучающей выборки и ОПХ
2. 3. Вычисление степени подобия ОПХ каждому из объектов обучающей выборки
2. 4. Степень уверенности в том, что ОПХ относится к какому-либо классу, присутствующему в обучающей выборке, есть среднее подобие ОПХ объектам обучающей выборки относящимся к данному классу.
Система распознавания образов, основанная на неявном задании классификационных правил, - это обучающая выборка с которой связана процедура, получающая на входе описание некоторого объекта и выдающая на выходе степень уверенности отнесения этого объекта к какому либо из классов, представленных в обучающей выборке.
Обучающая выборка - это индексированной множество CLASSES, элементы которого - индексированные множества, элементы которых - описания объектов относящихся к одному классу.
Описание объекта - это индексированное множество, элементы которого:
C - индексированное множество, элементы которого - описания каждого из признаков объекта DESC - матрица, строки которой используются для описаний каждого из состояний объекта. Способ описания состояний зависит от вида объекта. COND - вектор, элементы которого - степень нахождения объекта в одном из состояний, описанных соответствующей строкой DESC. Способ вычисления степени нахождения в каком либо состоянии (функция принадлежности к какому-либо состоянию) различен для разных видов объектов.
Объекты, по степени однотипности их признаков, делятся на объекты-не-контейнеры и объекты-контейнеры.
Объект-не-контейнер - это группа признаков, различных по смыслу.
Объект-контейнер(контейнерный объект, контейнер) - это группа однотипных объектов, выступающая как одно целое. Контейнеры, по степени взаимосвязи объектов, их составляющих, делятся на:
Вид объектов, состав их признаков, перечень возможных состояний определяется в процессе построения объектной модели каждой конкретной предметной области применения системы распознавания образов. Перечень возможных состояний объектов ограничен множеством, состоящим из всех возможных комбинаций различных признаков объекта и состояний каждого из них. Например, в случае объекта-не-контейнера, максимальное число возможных состояний равно:
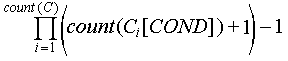
Действительно, в случае, например, объекта состоящего из двух признаков, каждый из которых имеет по два возможных состояния, максимальное число возможных состояний объекта равно восьми. Покажем через запятую, описания этих состояний(одна цифра - один элемент описания): 01, 02, 10, 20, 11, 12, 21, 22.
В случае, если классификационные правила априорно не известны, целесообразно учитывать в объектной модели предметной области как можно большее число возможных состояний объекта, так как это увеличивает шансы того, что в число этих состояний войдут состояний, удовлетворяющие неизвестным классификационным правилам.
Признаки объекта делятся на простые - значение которых представимо одним числом; и сложные - значение которых не представимо одним числом.
Описание простых признаков - индексированное множество, единственный элемент которого - вектор COND, каждый элемент которого - степень нахождения признака в одном из состояний.
Сложные признаки - суть объекты, входящие в состав некоторого супер-объекта. Описание сложного признака аналогично описанию объектов.
Перечень возможных состояний каждого, семантически отличного от других, признака объекта определяется в процессе построения объектной модели каждой конкретной предметной области применения системы распознавания образов.
Степень подобия двух объектов определяется как отношение объема пространства состояний, в которых находятся оба объекта, к объему пространства состояний, в которых находится хотя бы один из объектов.
Степень уверенности в принадлежности некоторого объекта, описание которого поступило на вход системы распознавания образов, к какому-либо классу - суть средняя величина подобия данного объекта объектам (описаниям этих объектов), обучающей выборки, относящихся к данному классу.
Покажем, что система распознавания образов, основанная на явном задании классификационных правил, представима в терминах системы с неявным заданием классификационных правил.
- Каждое из ЕСЛИ-ТО правил, содержащих дизъюнкцию, представимо эквивалентным ему множеством ЕСЛИ-ТО правил, не содержащих дизъюнкцию
- Каждое ЕСЛИ-ТО правило, не содержащее дизъюнкцию, представимо в виде описания отдельного состояния объекта.
- Все ЕСЛИ-ТО правила, не содержащие дизъюнкцию, используемые для всех классов данной предметной области, представленные в виде описаний состояний объекта, образуют перечень возможных состояний объекта.
- Описание объекта-шаблона некоторого класса - это описание объекта, находящегося во всех состояниях, соответствующих всем ЕСЛИ-ТО правилам данного класса; и не находящегося ни в одном из состояний, соответствующих какому-либо из ЕСЛИ-ТО правил любого другого класса.
- В обучающую выборку достаточно включить по описанию одного объекта-шаблона каждого из классов.
- Таким образом, мы привели систему распознавания образов, основанную на явном задании классификационных правил, к терминам системы с неявным заданием классификационных правил.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки