Решение задачи коммивояжёра рекурсивным полным переборомСформулируем задачу.
Дано N узлов, расположенных на плоскости. Задан входной узел (Вх) и выходной узел (Вых). Необходимо обнаружить кратчайший путь, охватывающий все узлы, начинающийся во входном узле, заканчивающийся в выходном узле и проходящий через каждый узел только один раз.
Есть мнения, что задача коммивояжёра может формулироваться ещё двумя способами:
1. необходимо обнаружить кратчайший гамильтонов цикл
2. необходимо обнаружить кратчайший путь, начинающийся в заданном узле
Однако обе эти формулировки при ближайшем рассмотрении оказываются частными случаями первой формулировки.
Формулировка 1 подразумевает, что входным узлом может быть любой узел, а выходным - один из ближайших к нему. Что требует полного перебора всех ближайших узлов к произвольно выбранному узлу.
Формулировка 2 подразумевает, что входной узел задан, а выходным узлом может быть любой. Что требует полного перебора всех выходных узлов с последующим выбором кратчайшего пути из всех кратчайших.
Поэтому мы остановимся на первоначальной формулировке, и будем решать задачу в общем виде.
Совершенно очевидно (кому не очевидно, может проверить и убедиться), что задача коммивояжёра в общем случае гарантированно решается оптимально только полным перебором всех вариантов.
В алгоритмической реализации полного перебора возможно применение двух условий, сокращающих время перебора и отсекающих заведомо неоптимальные пути, а именно:
1. При построении очередного варианта пути, подсчитывать его длину и если эта длина превышает уже найденный локальный минимум длины – пропускать этот вариант и все те, которые он порождает.
2. Если следующее выбранное ребро пересекает одно из ранее построенных рёбер – пропустить этот вариант и все те, которые он порождает.
Последнее условие фактически запрещает циклы, т.к. если мы представим себя на месте реального коммивояжёра, то пересечение рёбер (несмотря на то, что в задаче запрещено в явном виде только повторное использование узлов) фактически будет означать возврат коммивояжёра в то место, где он уже был, что противоречит определению оптимального (кратчайшего) пути.
Кроме этого, следует подумать о таком способе оптимизации как уход от вычисления точной длины пути в процессе его поиска. Ведь нам, в сущности, не интересно знать точную длину гипотенузы. Нам интересно знать, какая гипотенуза длиннее для двух данных пар катетов…
Оптимальное решение задачи коммивояжёра на десктопах возможно. Однако с ростом количества узлов время, затрачиваемое на полный перебор, растёт экспоненциально. Таким образом, на машине с четырёхядерным процессором 2,67 ГГц 10 узлов обсчитывается в среднем за 5 миллисекунд, 20 узлов – за 15 минут, а на расчёт оптимального пути для 60 узлов уйдёт более 6 триллионов лет…
Для обхода этого препятствия люди просто отказываются от получения оптимального решения для больших N и вместо задачи коммивояжёра решают какую-то другую, очень похожую, аналогичную задачу. Такой метод подмены задачи получил название «эвристического решения», хотя эвристика в каждом случае – это не более чем случайно выбранная аналогия. Например, отжиг – это решение задачи путём имитации охлаждения кристаллизующихся веществ, жадный алгоритм – это имитация поведения жадного человека, существуют методы, построенные по аналогии с поведением муравьёв, надувающимся воздушным шариком и т.п.
Метод аналогии плох тем, что полный перебор, как оптимальный метод решения, отбрасывается полностью и полностью заменяется каким-то другим методом. Я считаю, что так пренебрежительно поступать с полным перебором нельзя, потому что это единственный метод, который гарантированно даёт правильное решение задачи.
Мы попробуем решать задачу коммивояжёра только полным перебором, заменяя его чем-то другим только там, где это действительно необходимо из соображений экономии времени.
Мы не будем искать аналогию наугад, мы попробуем решить задачу коммивояжёра максимально непредвзято, не призывая на помощь посторонние аналогии. Попробуем решить общую задачу в общем виде. А для этого призовём на помощь только одну аналогию - аналогию с интеллектом вообще. Как решает сложные задачи (в том числе и задачу коммивояжёра) человеческий интеллект? Он разбивает исходную задачу на дерево более простых под-задач, решает их в обратном порядке и получает результат. Мы поступим точно так же!
Совершенно очевидно, что упростить задачу коммивояжёра для того, чтобы решать её полным перебором за приемлемое время, можно только одним способом – уменьшить количество перебираемых узлов. А это возможно сделать тоже только одним способом – объединить узлы в группы – над-узлы, над-задачи (суб-задачи).
Чтобы поставить задачу коммивояжёра рекурсивно попробуем взглянуть на неё рекурсивно.
Основной элемент в этой задаче – это узел, в который входит одно ребро и выходит одно ребро:
Не призывая посторонние аналогии, мы тут же замечаем аналогию с самой постановкой общей задачи, в которой задано два «крайних» узла:
Вх, в который входит коммивояжёр на старте, и
Вых, из которого выходит коммивояжёр на финише. Можно сказать, что вся совокупность узлов N в задаче – это один большой узел, в который коммивояжёр входит и выходит по ребру:
Таким образом, вырисовывается общий вид рекурсивного алгоритма.
1. Задать узлы N.
2. Задать максимально допустимое время решения задачи Tmax.
3. Провести на данной машине бенчмарк и определить зависимость времени решения от количества узлов при полном переборе вариантов Т(N).
4. Исходя из заданного количества узлов N, Tmax и зависимости для Т определить, на сколько групп (над-узлов) следует разбить множество из N узлов. Либо задать это количество узлов вручную (именно так мы и поступим).
5. Разбить множество из N узлов на M групп.
6. Провести
полный перебор для M групп и найти кратчайший путь для соединения этих групп.
7. После шага 6 у нас известно для каждой группы вход и выход, поэтому мы ставим рекурсивно задачу коммивояжёра для каждой группы, т.е. переходим к шагу 4, где N равно количеству узлов в каждой группе.
8. После выхода из рекурсии получаем подоптимальный путь для данной машины и данного Tmax (либо заданного количества узлов в группе).
Пункт 4 нужен для того, чтобы мы не ухудшали алгоритм сверх необходимого. Если машина может провести полный перебор для данного количества узлов, то мы должны ей это позволить.
На шаге 5, очевидно, лучше предпочитать M как можно больше. При М стремящемся к N мы получаем всё более точное решение. Чем меньше мы уходим от полного перебора, тем точнее наше решение. Выбрать M можно по таблице, составленной из самого простого грубого предположения, что на каждом шаге рекурсии мы будем разбивать суб-задачу на группы с одинаковым количеством узлов в группе.
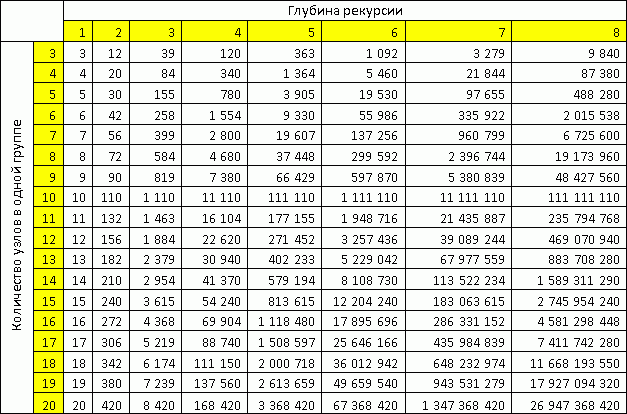
Как видно из таблицы, уже при 18 узлах в одной группе мы можем обрабатывать более 10 миллиардов узлов при глубине рекурсии до 8.
Если мы хотим улучшить найденный таким образом маршрут, то у нас есть такие варианты:
- выбрать более производительную машину
- увеличить допустимое время Tmax
- увеличить количество групп
- увеличить вложенность рекурсии. То есть на шаге 6 разбивать задачу на существенно (в зависимости от N) большее число групп, но производить их перебор не оптимально, а подоптимально. Например, разбивать задачу из 1000 узлов на 500 групп, но искать не кратчайший путь их соединения полным перебором (это слишком долго), а разбивать группы на суб-группы, например по 250 групп и проводить поиск подоптимального пути среди них. И так далее, пока мы не спустимся на уровень, где машина может сделать полный перебор.
Как объединять узлы в группы?Чтобы не привлекать «с потолка» отвлечённые аналогии и не пользоваться эвристиками, попробуем найти ответ в самой задаче. Совершенно ясно, что изначально в задаче у нас одна группа, для которой заданы Вх и Вых.
Чтобы разбить данную задачу минимум на две, нам необходимо выделить среди всех узлов промежуточный узел, который станет промежуточным входом/выходом.
Поскольку в качестве признака оптимальности в задаче мы применяем евклидово расстояние, то для обнаружения нового промежуточного входа/выхода нам необходимо ввести некий лимит расстояния от каждого узла до уже существующих входа и выхода. Поскольку мы не знаем, что это за лимит возьмём его настолько большим, чтобы оказалось, что все узлы принадлежат только начальной группе. Теперь будем плавно уменьшать этот лимит. При этом один из узлов ранее принадлежавший первоначальной группе должен выделиться. Независимо от того, что именно мы возьмём в качестве лимита, этим узлом станет тот узел, который расположен на самом дальнем расстоянии от первоначальных входа и выхода. Поэтому вместо выдумывания формулы лимита мы можем сразу брать самый дальний узел. После того как мы нашли этот промежуточный вход/выход, мы должны поделить все оставшиеся узлы между новыми двумя группами так, чтобы гарантировать непересечение ребёр.
Если нам надо поделить задачу на произвольное число групп, то мы производим это разбиение рекурсивно. Сначала находим промежуточный вход/выход взаимо-дальний по отношению к начальным входу и выходу. Потом находим второй промежуточный вход/выход взаимо-дальний к первым трём, и так далее.
Очевидно, что при количестве групп, равному N, промежуточные входы/выходы этих групп совпадут с начальными узлами. Таким образом, мы нашли единственно правильное деление всех узлов на группы.
Поиграться с разбиением на группы можно
здесь.
Чтобы создать задачу коммивояжёра нужно ввести количество узлов и нажать Enter. Либо загрузить задачу из файла.
Перемещая ползунок можно наблюдать принцип разбиения на группы. Кнопка «Link groups» соединяет текущие группы по оптимальному маршруту полным перебором. Кнопка «Link nodes» соединяет все узлы по оптимальному маршруту полным перебором. Поэтому не следует давить эти кнопки при большом (>18) количестве узлов или групп.
Здесь можно скачать программу для решения задачи коммивояжёра по алгоритму, описанному выше.
Органы управления:
Кнопка «Load» загружает задачу из файла с расширением *.txt
Формат файла txt такой: в каждой строке через 1 пробел указаны координаты x и y для каждого узла в задаче. В первой строке указаны координаты входного узла. В последней строке – координаты выходного узла. Остальные узлы между ними в произвольном порядке. Координаты находятся в диапазоне 0-1 с точностью 6 знаков после запятой. Отделитель целой и дробной части – запятая.
Кнопка «Generate» генерирует рандомом случайную задачу коммивояжёра, с количеством узлов, указанном в поле «Nodes =».
Кнопка «Save» сохраняет координаты узлов данной задачи.
Кнопка «Solve» решает задачу коммивояжёра, рекурсивно разбивая её на константное количество групп, указанном в поле «Groups =». Если заданное количество групп больше либо равно количеству узлов, то будет, естественно, производится полный перебор узлов. Поэтому не рекомендуется указывать количество групп более 18.
В данной программе разбивка на группы не оптимальная, поэтому пересечения случаются. Но этот недостаток принципиально устраним.