|
В 1949 физиолог Дональд Олдингс Хебб (как же
беднягу, наверное, обзывали в школе!) написал
книгу "Организация сознания". В этой книге
он попытался объяснить, как нейроны
человеческого мозга могут обучаться. Его теория
получила впоследствии название "Обучение
Хебба".
Основное утверждение
теории: два нейрона мозга могут иметь связь
(соединение) друг с другом. Нейроны могут
принимать активное или пассивное состояние. Если
оба нейрона активны в одно и то же время, то сила
связи между ними возрастает. Если хотя бы один
нейрон не активен, то сила связи не
увеличивается. Такая теория приобрела название
Усиления Длительной Связи (Long Term Potentiation).
Впоследствии эта предельно простая теория была
расширена как самим Хеббом, так и другими
исследователями. Еще одно правило было добавлено
- "нехеббовское обучение" (antihebbian learning). Здесь
добавлено предположение, что если из двух
нейронов только один активен, то сила связи не
только не увеличивается, но и уменьшается. Если
оба нейрона неактивны, то сила связи не
изменяется (Подавление Длительной Связи – Long Term Depression).
Нейрон, подающий
сигнал второму нейрону принято называть
пресинаптическим, а нейрон-приемник –
постсинаптическим:
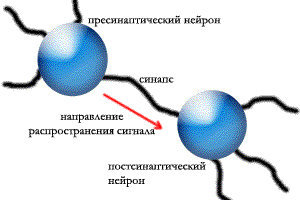
В виде таблицы взаимоотношение нейронов можно представить так:
| состояние первого нейрона |
состояние второго нейрона |
влияние на связь между нейронами |
| неактивен |
неактивен |
не влияет |
| неактивен |
активен |
подавление |
| активен |
неактивен |
подавление |
| активен |
активен |
усиление |
Вообще говоря, Хебб пошел в своих
идеях еще дальше модифицирования связей. Он
предположил, что отдельные нейроны или отдельные
группы нейронов могут передавать сигнал со своих
выходных элементов на свои же входные элементы,
формируя тем самым реверберирующие структуры:
нейрон A возбуждает нейрон B,
который возбуждает нейрон C, который в свою очередь
возбуждает нейрон A.
Такие структуры могут объяснить явление накопления усталости нейронов.
Также Хеббу принадлежит и идея о группировании
клеток, которой посвящено отдельное направление
исследований.
Используя идеи Хебба
об усилении и подавлении весов связей, мы можем
построить модель простой хеббовской связи между
двумя нейронами. То, что мы моделируем, не
является нейронами как таковыми, а связями между
ними. Таким образом, одинарное соединение
выражается с помощью единственного
действительного числа – что может быть проще?
Конечно же, получить
приемлемые результаты с помощью одной связи
невозможно, поэтому мы будем составлять модель
из множества связей. Возможная ситуация, когда
требуется такая хеббовская сеть: пусть на входе
имеется поверхность, разбитая на квадраты (5х5). На
эту поверхность мы накладываем схематическое
изображение лица человека (веселый/грустный).

Мы хотим заставить
хеббовскую сеть различать выражения лица, т.е. на
выходе имеется значение 1 для веселого типа и 0 -
для грустного. Здесь требуются хеббовские связи
между 25 входными элементами и 1 входным. Чуть позже будет описана
ситуация с несколькими выходными элементами.
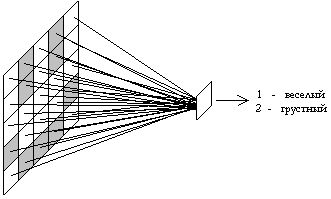
Вся сеть смоделирована 25 числами, каждое из
которых инициализируется каким-то случайным
числом, например между 0 и 1:
var strengths : array [1..5,1..5] of real;
procedure initialise_strengths;
var i,j : integer;
begin
for i:=1 to 5 do
for j:=1 to 5 do
strengths[i,j]:=random(1000)/1000
end;
|
Функция random(1000)
возвращает случайное число в диапазоне от 0 до 999,
выражение random(1000)/1000 позволяет получить
дествительное число в диапазоне от 0 до 0.999.
Будьте внимательны, если работаете в C++ или
подобном языке – как random(1000),
так и 1000 - целые числа, так что компилятор может
автоматически выбрать целочисленное деление, а
результат такого деления в данном случае - 0.
Любителям языка C++ лучше писать строку как
random(1000)/1000.0 .
После инициализации
связей можно приступать к обучению сети: подаем
на вход изображение, желаемый результат на выход
и соответствующим образом модифицируем связи.
Это приводит к проблеме выбора обучающих правил.
Если мы просто используем идею об усилении
связей (не используя при этом уменьшение связей),
то мы должны использовать формулу:
dw = n ai aj
в данном случае
dw – изменение веса связи между i входным элементом и выходным элементом j,
ai – уровень сигнала на входном элементе i,
aj – уровень сигнала на выходном элементе j,
n – постоянный множитель, предохраняющий от слишком значительных изменений весов связей.
Например, предположим,
что вес связи между входным и выходным нейроном
на текущий момент равен 0.75. Установим активность
входного нейрона равной 0.5, а выходного - 0.2. Если константа равна
0.01, то вес изменится (увеличится) на значение 0.5x0.2x0.01=0.001 (т.е. вес связи станет
равным 0.751). Ниже приведен код для обновления всех весовых
коэффициентов для данной задачи. Входные данные
хранятся в массиве ipt[], а выходное значение хранится в переменной opt:
const ETA = 0.01;
var ipt : array [1..5,1..5] of real;
procedure update_strengths;
var i,j : integer;
begin
for i:=1 to 5 do
for j:=1 to 5 do
strengths[i,j]:=strengths[i,j] + ETA * ipt[i,j] * opt;
end;
|
Понятно, что при значениях входных и выходных данных, больших 0,
весовые коэффициенты не могут уменьшаться, - они
принимают все большие и большие значения. Здесь правило Хебба необходимо расширить. Если
вышеприведенную формулу привести к виду:
dw = n(2ai - 1) aj,
то веса будут уменьшаться при
активностях входных элементов, меньших 0.5 ( 2ai-1 будет
давать отрицательное число). Эта ситуация
называется Post-Not-Pre LTD (пост-непре-синаптическое
подавление длительной связи) в том смысле что вес
связи будет уменьшаться при неактивном
пресинаптическом нейроне и активном
постсинаптическом.
Формула также может быть написана в другом виде:
dw = n ai (2aj - 1)
В этом случае вес связи уменьшается при активном пресинаптическом
нейроне и неактивном постсинаптическом, т.е. мы
имеем так называемый непост-пре-синаптическое
подавление связи.
При желании можно пойти дальше, и объединить оба случая в одном уравнении:
dw = n (2ai - 1) (2aj - 1)
но по скорому размышлению мы понимаем
ошибочность такого объединения, - если входной
нейрон неактивен и неактивен выходной нейрон (те
имеют уровни активности в диапазоне от 0 до 0.5),
произведение отрицательных чисел дает
положительное число, и вес связи увеличивается!
Поэтому используйте только одну модель, в
зависимости от того, какая больше подходит под
конкретную ситуацию.
Вот модифицированный кусок кода для
обновления весовых коэффициентов. Я включил сюда
переменную, задающую используемый тип
подавления связей:
const ETA = 0.01;
LTP = 1;
POST_NOT_PRE = 2;
PRE_NOT_POST = 3;
var ipt : array [1..5,1..5] of real;
train_type : integer;
procedure update_strengths;
var i,j : integer;
begin
for i:=1 to 5 do
for j:=1 to 5 do
case train_type of
LTP : strengths[i,j]:=strengths[i,j] + ETA * ipt[i,j] * opt;
POST_NOT_PRE : strengths[i,j]:=strengths[i,j]
+ ETA * (2*ipt[i,j]-1) * opt;
PRE_NOT_POST : strengths[i,j]:=strengths[i,j]
+ ETA * ipt[i,j] * (2*opt-1)
end
end;
|
Должны ли веса связей принимать
значения в диапазоне от 0 до 1? В правилах Хебба
нет ни слова о том, что веса связей не могут
принимать отрицательные значения или
увеличиваться до бесконечности. Если
возникла необходимость ограничения, следует
дописать пару строчек кода (выделены
курсивом):
procedure update_strengths;
var i,j : integer;
begin
for i:=1 to 5 do
for j:=1 to 5 do
case train_type of
LTP : strengths[i,j]:=strengths[i,j] + ETA * ipt[i,j] * opt;
POST_NOT_PRE : strengths[i,j]:=strengths[i,j]
+ ETA * (2*ipt[i,j]-1) * opt;
PRE_NOT_POST : strengths[i,j]:=strengths[i,j]
+ ETA * ipt[i,j] * (2*opt-1)
end;
if strengths[i,j] > 1
then strengths[i,j]:=1;
if strengths[i,j] < 0
then strengths[i,j]:=0
end;
|
Не забывайте о необходимости вызывать процедуру обновления
весов update_strengths многажды, так чтобы весовые коэффициенты были в итоге приведены к своим
конечным значениям:
for training_run := 1 to 10000 do
for pattern := 1 to NUM_TRAINING_PATTERNS do
begin
copy_input(pattern);
update_strengths
end;
|
Обычно хеббовские
нейронные сети обучаются очень медленно. Вы
можете убедиться в том, что часто входные образы
приходится предъявлять тысячами раз и несмотря
на это, сеть может обучаться неверно. Если
имеется, к примеру, 8 обучающих образов то
придется предъявить один образ, модифицировать
веса и повторить
процедуру для всех остальных образов, а затем
повторять и повторять этот цикл столько раз,
сколько потребуется для получения правильных
результатов.
Получение результатов. Установив весовые
коэффициенты можно приступить к работе
непосредственно над распознаванием символов,
что заключается в предъявлении сети входных
образов, умножении каждого входного элемента на
вес связи и суммировании результатов. Так мы
получаем ответ сети, который не будет равен ровно
0 или ровно 1, но в лучшем случае будет лежать
достаточно близко к ним. Т.е. если ответ сети
больше 0.5 то сеть классифицирует изображение как
счастливое лицо, если меньше - как недовольное
жизнью.
procedure run_net;
var i,j : integer;
sum : real;
begin
sum:=0;
for i:=1 to 5 do
for j:=1 to 5 do
sum := sum + strengths[i,j] * ipt[i,j];
if sum > 0.5
then writeln('This is a happy face.')
else writeln('This is a sad face.')
end;
|
Двухмерные сети Хебба. Довольно легко увеличить количество
выходных элементов, для этого выходная переменная opt заменяется на массив opt[],
представляющий выходную сетку:
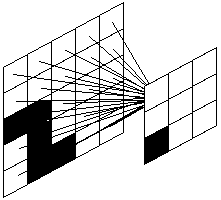
На этом рисунке я показал связи, идущие от входных элементов к одному выходному
потому, что иначе рисунок был бы слишком неразборчив. На самом деле все выходные элементы
связаны со входными, и массив весов связей strengths[] теперь имеет 4
измерения, а не 2. Так strengths[a,b,c,d] будет обозначать вес
связи между входным элементом [a,b] и выходным элементом [c,d]. Несмотря на это, новый код
немногим отличается от прежнего:
var strengths : array [1..5,1..5,1..3,1..3] of real;
procedure initialise_strengths;
var i,j,k,l : integer;
begin
for i:=1 to 5 do
for j:=1 to 5 do
for k:=1 to 3 do
for l:=1 to 3 do
strengths[i,j,k,l]:=random(1000)/1000
end;
procedure update_strengths;
var i,j,k,l : integer;
begin
for i:=1 to 5 do
for j:=1 to 5 do
for k:=1 to 3 do
for l:=1 to 3 do
case train_type of
LTP : strengths[i,j,k,l]:=strengths[i,j,k,l]
+ ETA * ipt[i,j] * opt[k,l];
POST_NOT_PRE : strengths[i,j,k,l]:=strengths[i,j,k,l]
+ ETA * (2*ipt[i,j]-1) * opt[k,l];
PRE_NOT_POST : strengths[i,j,k,l]:=strengths[i,j,k,l]
+ ETA * ipt[i,j] * (2*opt[k,l]-1)
end;
if strengths[i,j,k,l] > 1
then strengths[i,j,k,l]:=1;
if strengths[i,j,k,l] < 0
then strengths[i,j,k,l]:=0
end;
procedure run_net;
var i,j,k,l : integer;
result : array [1..3,1..3] of real;
begin
for k:=1 to 3 do
for l:=1 to 3 do
begin result[k,l]:=0;
for i:=1 to 5 do
for j:=1 to 5 do
result[k,l] := result[k,l] + strengths[i,j,k,l] * ipt[i,j]
end;
end;
|
Вы видите, что выходная сетка
необязательно должна быть того же размера (и
может иметь иные очертания), что и входная. В
приведенном примере выходная сетка имеет
размерность 3-на-3, а входная – 5-на-5.
Основное отличие заключается в
процедуре получения результатов. Теперь мы уже
не можем просто суммировать взвешенные входные
значения, а должны сравнивать полученную в
результате вычислений сетку числовых значений с
эталонными выходными сетками (эталонными
образцами). Те эталонные сетки, которые наименее
отличаются от полученных и являются ответами
сети.
В исходных текстах дан пример сети
Хебба, которая была обучена на задаче типа
«что-где» (простая фигура произвольно расположена на сетке, а
сеть должна ее идентифицировать (ответить на
вопрос «что?») и сказать, где она находится
(вопрос – «где?»)). Надо заметить, что на второй
вопрос сеть Хебба успешно отвечает, но вот первый
(идентификация фигуры) слишком сложен для столь
простой системы.
Что яйцеголовые говорят о связях Хебба? Вы хотите прочесть
книгу Хебба? Должен Вас предупредить, что она
написана весьма занудным стилем. Есть также и
другие книги Хебба, датированные после 1949 года.
Мне также известно, что Хебб был заслуженным профессором в 1949, - представьте,
сколько ему исполнилось в 1980!
Hebb, D. O. (1949) "Organisation of Behavior", pub. John Wiley & Sons, New York.
Hebb, D. O. (1980) Essay on Mind pub. Erlbaum, Hillsdale, NJ.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки