|
Ученые, занимающиеся
нейронными сетями, говорят, что человеческий
мозг состоит из миллионов специализированных
клеток - нейронов. Существует множество разных
типов нейронов, но все они действуют по одному
принципу:
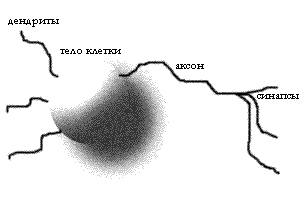
Тело клетки принимает сигналы от других
нейронов через отростки (слева) - так называемые
дендриты (т.к. они похожи на ветви дерева). Нейрон
анализирует сигнал, и когда уровень сигнала
достигает некоторого порогового значения,
нейрон срабатывает, передавая другим клеткам его
через связи на конце аксона, - синапсы, которые, в
свою очередь присоединены к дендритам других
клеток.
При программной реализации эта модель
упрощается. В основном, используется следующая
схема:

Нейрон обозначен окружностью в центре
рисунка. У него есть несколько входов (линии
слева) (реальные клетки мозга могут иметь тысячи
таких входов) и единственный выход (линия справа).
Нейроны связаны друг с другом таким образом, что
выходы одних подсоединены ко входам других
нейронов. Если Вы сравните компьютерную модель с
приведенным рисунком, то увидите, что синапсы
исчезли, - это компенсируется тем, что несколько
других нейронов используют в качестве входа
непосредственно выход этого нейрона.
В человеческом мозге под сигналами
понимаются химические связи между узлами. Сигнал
формируется в клетке, а затем
"выстреливается" из нее. После этого клетка
готова к формированию следующего сигнала.
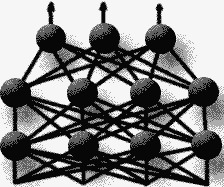
В человеческом мозге нейроны
соединены в сверхсложные сети с неисчислимым
множеством переплетений связей. Искусственные
сети имеют гораздо более простую структуру.
Самая распространенная - многослойный
персептрон с прямым распространением, в котором
нейроны объединены в слои, выходы нейронов
одного слоя подсоединены ко входам нейронов
следующего слоя:
Обычно в сети имеется три слоя (в
принципе можно доказать, что больше вряд ли
потребуется), - входной слой, скрытый слой и
выходной слой.
Каждая связь между узлами
характеризуется силой связи, обозначающей
степень воздействия связи на результат расчета.
Информация, запоминаемая сетью находится именно
в массиве весовых коэффициентов.
Определим некоторые термины.
Чуть раньше я упоминал термин прямое
распространение. Это означает, что сигнал от
одного слоя к другому может распространяться
только в одном направлении, т.е. возможна
передача сигнала из слоя 1 в слой 2, из слоя 2 в слой
3 и т.д., передача в иных направлениях -
отсутствует. Противоположностью прямого
распространения является рекуррентная сеть, у
которой имеются соединения с обратной связью:
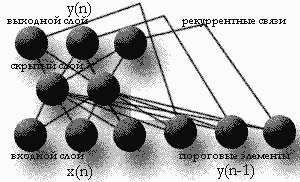
В рекуррентных сетях часто
встречается понятие предпочтительных состояний
- сигналы проходят по сети, возвращаются на
входные слои и изменяются до тех пор, пока не
превратятся в повторяющийся стабильный набор
значений. Входные сигналы изменяются вплоть до
достижения предпочтительных состояний, после
достижения - считаются достигшими стабильности.
Главный секрет рекуррентных сетей -
модифицирование весов до конкретных
предпочтительных значений.
Одна из проблем нейронных сетей, -
линейная разделимость или линейная
неразделимость области данных. Рассмотрим
простой пример. Допустим имеется нейронная сеть
с 2 входными элементами и одним выходным
элементом:
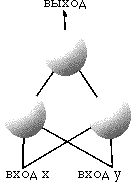
Я пометил входы сети как x и y, чтобы мы
могли представить их как координаты на графике.
Предположим, что на выходе требуется получить 1
при входном x>y (в противном случае на выходе
требуется получить 0). График может быть поделен
на 2 области:
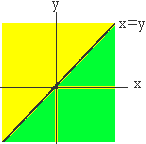
Желтая область представляет все
комбинации x и y, которые должны давать на выходе 1,
зеленая область - комбинации с нулевым
результатом. Этот тип классификации носит
название линейно разделимого, т.к. между этими
областями можно провести прямую.
Иначе дело обстоит, если нужно
получить единичный выход при x и y, принадлежащих
одному знаку (обе переменные положительны или
обе отрицательны), и нулевой выход для
несовпадающих по знаку переменных:

Такая ситуация называется линейно
неразделимой, между областями невозможно
провести разделяющую прямую. Необходимо
заметить, что линейно разделимые ситуации в
отличие от неразделимых легче воспринимаются
нейронными сетями при обучении. Существуют типы
сетей (простые персептроны и сети Хебба,
например), которые в принципе необучаемы линейно
неразделимым ситуациям.
|
 материалы
материалы  справочник
справочник  форум
форум  гостевая
гостевая  ссылки
ссылки