Программная реализация нейронов

Я описывал каждый отдельный нейрон как запись, содержащую все необходимые части:

• Список весовых коэффициентов для связей между данным нейроном и всеми нейронами предыдущего слоя (или входными данными, если нейрон находится во входном слое). Каждый весовой коэффициент - действительное число (по 1 весовому коэффициенту на нейрон предыдущего слоя)
• Пороговый уровень (см. далее) (см. также примечание переводчика в конце главы)
• Значение ошибки. Используется только на стадии обучения. Эта величина необязательно дожна быть связана с нейроном, я сделал это только для удобочитаемости кода.
• Изменение ошибки. Также используется только во время обучения.

Вот само описание нейрона:

const NUM = 10; {или любое другое! - количество нейронов
                 в предыдущем слое. Изменяется в зависимости от того, в каком
                 слое находится рассматриваемый нейрон}
type
    weights_type = array [1..NUM] of real;
    neuron_type = record
                      w : weights_type;      {весовые коэффициенты}
                      a : real;              {сигнал на выходе нейрона}
                      threshold : real;
                      E : real               {значение ошибки}
                      change : weights_type; {используется в процессе обучения}
                      t_change : real;       {аналогично}
                  end;

Выходной сигнал нейрона хранится в поле a (так называемая активность нейрона). Нейрон должен отреагировать на входной сигнал, поступающий по взвешенным связям, вычислив при этом выходной сигнал. Для трансформации входных сигналов в выходные необходима функция.

Ниже приведена декларация узлов с помощью переменных. Постоянные обозначают количество нейронов во входном, скрытом и выходном слое:

const MAX_INP = 4; {количество нейронов в каждом слое} MAX_HID = 4; MAX_OUT = 2; var ipl : array [1..MAX_INP] of neuron_type; hl : array [1..MAX_HID] of neuron_type; ol : array [1..MAX_OUT] of neuron_type;

Активационные (переходные) функции

На протяжении ряда лет для превращения входных сигналов в выходные использовалось несколько типов функций. На приведенных ниже рисунках показаны графики некоторых из наиболее часто используемых. По горизонтали - сумма входных сигналов (см. ниже), по вертикали - значение функции. Все функции выдают результат в диапазоне от 0 до 1.

	Простая ступенчатая (шаговая) функция. Значение активационной функции равно 1 при положительной сумме входных сигналов или 0 при отрицательной.
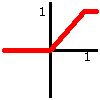	Функция, значение которой равно 0 при отрицательном аргументе, при положительном аргументе - пропорционально аргументу (только до 1).
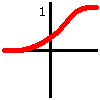	Так называемая сигмоида. Значение функции стремится к 0 при больших отрицательных значениях, к 1 - при больших положительных, со сглаженным переходом между теми и другими. Сигмоидальная функция описывается уравнением:

Эта функция, как считается, наиболее точно описывает активность настоящих нейронов мозга и наиболее часто используется в искусственных нейронных сетях. Код на паскале для этой функции:

function sigmoid (x : real) : real;
begin 
    sigmoid := 1/(1 + exp(-x))
end;

Однако паскалевская функция exp приводит к ошибке в программе, если входное значение выходит из промежутка -39..38. К счастью, эти настолько значения далеко отстоят от начала координат, что мы можем считать: при аргументе < -39 значение функции равно 0, при аргументе > 38, - значение функции равно 1. Для предотвращения ошибки добавим несколько строчек:

function sigmoid (x : real) : real;
begin
    if abs(x) < 38 {отсеиваем "опасные" аргументы}
        then sigmoid := 1/(1+exp(-x)) 
        else if x >= 38 {наше допущение для аргументов меньших -39 и больших 38}
                then sigmoid := 1
                else sigmoid := 0
end;

Пороговое значение

На практике настоящие нейроны не срабатывают (не выдают выходной сигнал) до тех пор, пока уровень входного сигнала не достигнет некоторого порогового значения, т.е. на вход нейрона поступает сумма взвешенных сигналов минус некоторая величина. Полученное значение проходит через активационную функцию. Таким образом, общая формула выглядит так:

где
a - активность нейрона,
a_i - активность i-ого нейрона предыдущего слоя (или i-ое входное значение, если мы вычисляем активность нейрона входного слоя),
w_i - вес связи между данным нейроном и i-ым нейроном предыдущего слоя.

Каждая активность нейрона предыдущего слоя умножается на соответствующий весовой коэффициент, результаты умножения суммируются, вычитается пороговое значение, вычисляется значение сигмоидной функции. Вот пример на турбо паскале:

procedure run_network;
var 
    i,j : byte; {счетчики для циклов 'for'}
    sum : real;
begin
{Обходим все нейроны входного слоя. Вычисляем сумму
 взвешенных сигналов для входного набора данных}
for i:=1 to MAX_INP do
    with ipl[i] do {i-ый нейрон входного слоя}
        begin 
            sum:=0;
            for j:=1 to NUM_INPUTS do
                sum:=sum + w[j] * test_pat[j];
            a:=sigmoid(sum - threshold)
        end;

{Обходим все нейроны скрытого слоя. Действуем так же,
 как с нейронами входного слоя}
for i:=1 to MAX_HID do
    with hl[i] do
        begin 
            sum:=0;
            for j:=1 to MAX_INP do
                sum:=sum + w[j] * ipl[j].a;
            a:=sigmoid(sum - threshold)
        end;

{Все то же самое для выходного слоя}
for i:=1 to MAX_OUT do
    with ol[i] do
        begin 
            sum:=0;
            for j:=1 to MAX_HID do
                sum:=sum + w[j] * hl[j].a;
            a:=sigmoid(sum - threshold);
        end;
end;

Эта процедура состоит из трех очень похожих друг на друга блоков, по блоку на каждый слой нейронной сети. Выражение "with" позволяет обращаться к полям записей без упоминания самой записи, т.е. кусок кода:

with ipl[i] do w[j]:=...

полностью аналогичен:

ipl[i].w[j]:=...

Каждый слой нейронов базируется на выходе предыдущего слоя (за исключением входного слоя, базирующегося непосредственно на предъявляемых сети входных данных (в коде - массив test_pat). Это значит, что значения входного слоя должны быть полностью расчитаны до вычисления значений скрытого слоя, которые в свою очередь, должны быть рассчитаны до вычисления значений выходного слоя.

Выходы нейронной сети - значения активностей (поле a) нейронов выходного слоя. Программа, симулирующая работу нейронной сети, в процессе обучения будет сравнивать их со значениями, которые должны быть на выходе сети.

Например, если нейронная сеть используется для того, чтобы определить, персона какого пола запечатлена на фотографии, то возможно существование двух нейронов в выходном слое: для мужского пола на выходе "М" должно появиться значение 1, а на выходе "Ж" - 0. Соответственно, при предъявлении сети женской фотографии, выходные нейроны выдают обратные значения ("М"=0, "Ж"=1). На практике, если на выходе "М" - число 0.0261, а на выходе "Ж" - число 0.9932, то сеть выдает заключение о том, что на фотографии - женское лицо (точных значений 1 или 0 вряд ли можно добиться).

Если вам каким-либо образом уже известны весовые коэффициенты, то следующую главу можете смело пропустить. В противном случае, вам все таки придется приступить к обучению сети и столкнуться с понятием обратного распространения ошибки...

В литературе более распространен несколько отличающийся подход к "пороговому уровню". Боулс использует именно слово "пороговый" (threshold), подразумевая биологическую сторону вопроса (т.е. природу реального нейрона). В литературе обычно используют другой термин - "смещение" (bias), обосновывая необходимость введения такой величины математически (обеспечивается смещение кривой графика относительно 0, а как следствие большая гибкость функции). Такое расхождение, однако, не приводит к коренным разногласиям в реализации и математическом аппарате.

Предыдущая

Оглавление

Следующая